练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    在△ABC中，B=30°，C=45°，c=
    		6
    ，则最短边长为（　　）
    A、1
    B、
    		2
    C、
    		3
    D、
    		6
    考点：余弦定理
    专题：解三角形
    分析：由题意判断得到b为最短边，根据sinB，sinC，以及c的值，利用正弦定理求出b的值即可．
    解答： 解：∵在△ABC中，B=30°，C=45°，c=
    		6
    ，
    ∴B为最小角，即b为最短边，
    则由正弦定理
    b
    sinB
    =
    c
    sinC
    得：b=
    csinB
    sinC
    =
    		6
    ×
    1
    2
    		2
    2
    =
    		3
    ，
    故选：C．
    点评：此题考查了正弦定理，三角形的边角关系，以及特殊角的三角函数值，熟练掌握正弦定理是解本题的关键．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知函数f（x）=
    x+1-a
    a-x
    （x≠a）．
    （1）证明：函数f（x）在区间（a，+∞）上是增加的；
    （2）当x∈[a+
    1
    2
    ，a+1]时，求函数f（x）的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （1）已知x，y都是正实数，比较x3+y3与x2y+xy2的大小；
    （2）解不等式ax2-（2a+1）x+2＜0，其中a＞0，a为常数．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    数列{
    1
    n(n+1)
    }的前n项和为Sn，则S99=（　　）
    A、
    100
    99
    B、
    99
    100
    C、
    100
    101
    D、
    98
    99

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    为了得到函数y=cos（2x-
    π
    6
    ）的图象，可以将y=sin2x的图象（　　）
    A、向左平移
    π
    6
    B、向左平移
    π
    3
    C、向右平移
    π
    6
    D、向右平移
    π
    3

    查看答案和解析>>

    科目：高中数学 来源： 题型：

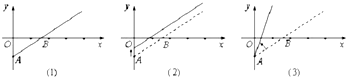    如图（1）是反应某公共汽车线路收支差额（即营运所得票价收入与付出成本的差）y与乘客两x之间关系的图象．由于目前该条公交线亏损，公司有关人员提出了两种调整的建议，如图（2）（3）的实线（虚线为原参考线）所示．给出下列说法：
    ①图（2）的建议是：提高成本，并提高票价；
    ②图（2）的建议是：降低成本，并保持票价不变；
    ③图（3）的建议是：提高票价，并保持成本不变；
    ④图（3）的建议是：提高票价，并降低成本．
    其中所有说法正确的是（　　）
    A、①③B、②③C、②④D、①④

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知函数f（x）=cos2x+
    		3
    sinxcosx，x∈R
    （1）求函数f（x）的最小正周期；
    （2）当函数f（x）取得最大值时，求自变量的集合；
    （3）用五点法作出函数f（x）在一个周期内的图象．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知cos（
    π
    6
    -θ）=a（|a|≤1），求cos（
    5π
    6
    +θ）和sin（
    2π
    3
    -θ）的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    命题“?x∈R，x2+x≥2”的否定是（　　）
    A、?x0∈R，x2+x≤2
    B、?x0∈R，x2+x＜2
    C、?x∈R，x2+x≤2
    D、?x∈R，x2+x＜2

    查看答案和解析>>

    同步练习册答案