练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】2019年春节假期，旅游过年持续火爆.特别是：东北雪乡、梦回大唐、江南水乡、三亚之行这四条路线受到广大人民的热播.现有2个家庭准备去这四个地方旅游，假设每个家庭均从这四条路线中任意选取一条路线去旅源，则两个家庭选择同一路线的概率为（ ）

    A.B.C.D.

    【答案】C

    【解析】

    分别设“东北雪乡、梦回大唐、江南水乡、三亚之行”为A，B，C，D，可列出两个家庭的选择的所有情况，及两个家庭选择同路线的情况，结合古典概型的概率公式可求出答案.

    分别设“东北雪乡、梦回大唐、江南水乡、三亚之行”为A，B，C，D.

    则两个家庭的选择有“AA，AB，AC，AD，BA，BB，BC，BD，CA，CB，CC，CD，DA，DB，DC，DD”共16种情况，

    其中满足两个家庭选择同路线的情况有“AA，BB，CC，DD”，共4种，

    所以两个家庭选择同一路线的概率为．

    故选：C.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】某鲜花店根据以往某品种鲜花的销售记录，绘制出日销售量的频率分布直方图，如图所示．将日销售量落入各组区间的频率视为概率，且假设每天的销售量相互独立．

    （1）求在未来的连续4天中，有2天的日销售量低于100枝且另外2天不低于150枝的概率；

    （2）用表示在未来4天里日销售量不低于100枝的天数，求随机变量的分布列和数学期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆的左焦点为，是椭圆上关于原点对称的两个动点，当点的坐标为时，的周长恰为．

    （1）求椭圆的方程；

    （2）过点作直线交椭圆于两点，且 ，求面积的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，已知四边形ABCD是边长为2的菱形，∠ABC=60°，平面AEFC⊥平面ABCD，EF∥AC，AE=AB，AC=2EF.

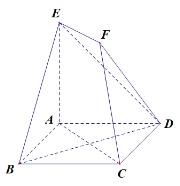
    （1）求证：平面BED⊥平面AEFC；

    （2）若四边形AEFC为直角梯形，且EA⊥AC，求二面角B-FC-D的余弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】(导学号：05856310)

    已知函数f(x)＝x＋＋ln x(a∈R)．

    (Ⅰ)当a＝2时， 求函数f(x)的单调区间；

    (Ⅱ)若关于x的函数g(x)＝－f(x)＋ln x＋2e(e为自然对数的底数)有且只有一个零点，求实数a的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在直角坐标系xOy中，直线l的参数方程为（其中t为参数）.以坐标原点O为极点，x轴非负半轴为极轴建立极坐标系，曲线C的极坐标方程为．

    （1）求l和C的直角坐标方程．

    （2）设点，直线l交曲线C于A，B两点，求的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知，（，），且的图象上相邻两条对称轴之间的距离为．

    （1）求函数的单调递增区间；

    （2）若的内角，，的对边分别为，，，且，，，求，的值及边上的中线．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】选修4-4：坐标系与参数方程

    在平面直角坐标系中，直线的参数方程为（为参数）.以原点为极点，轴的正半轴为极轴建立极坐标系，且曲线的极坐标方程为.

    （1）写出直线的普通方程与曲线的直角坐标方程；

    （2）设直线上的定点在曲线外且其到上的点的最短距离为，试求点的坐标.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，.

    （1）讨论的单调性；

    （2）定义：对于函数，若存在，使成立，则称为函数的不动点.如果函数存在不动点，求实数的取值范围.

    查看答案和解析>>

    同步练习册答案