
°æƒø°øƒœ±±≥Ø ±¥˙µƒŒ∞¥Û ˝—ߺ“◊Êïú‘Ğ ˝—ß…œ”–Õª≥ˆπ±œ◊£¨À˚‘Ğ µº˘µƒª˘¥°…œÃ·≥ˆ◊Êïú‘≠¿Ì£∫°∞√ı ∆º»Õ¨£¨‘Úª˝≤ª»ı“Ï°±.∆‰∫¨“ «£∫º–‘Ğ¡Ω∏ˆ∆Ω––∆Ω√Ê÷ƺ‰µƒ¡Ω∏ˆº∏∫ŒÃ£¨±ª∆Ω––”Ğ’‚¡Ω∏ˆ∆Ω√ʵƒ»Œ“‚∆Ω√ÊÀ˘Ωÿ£¨»Áπ˚Ωÿµ√µƒ¡Ω∏ˆΩÿ√ʵƒ√ʪ˝◊İœ‡µ»£¨ƒ«√¥’‚¡Ω∏ˆº∏∫ŒÃµƒÃª˝œ‡µ»£¨»ÁÕº£¨º–‘Ğ¡Ω∏ˆ∆Ω––∆Ω√Ê÷ƺ‰µƒ¡Ω∏ˆº∏∫ŒÃµƒÃª˝∑÷±Œ™![]() £¨±ª∆Ω––”Ğ’‚¡Ω∏ˆ∆Ω√ʵƒ»Œ“‚∆Ω√ÊΩÿµ√µƒ¡Ω∏ˆΩÿ√ʵƒ√ʪ˝∑÷±Œ™
£¨±ª∆Ω––”Ğ’‚¡Ω∏ˆ∆Ω√ʵƒ»Œ“‚∆Ω√ÊΩÿµ√µƒ¡Ω∏ˆΩÿ√ʵƒ√ʪ˝∑÷±Œ™![]() £¨‘Ú°∞
£¨‘Ú°∞![]() ◊İœ‡µ»°± «°∞
◊İœ‡µ»°± «°∞![]() œ‡µ»°±µƒ£® £©
œ‡µ»°±µƒ£® £©
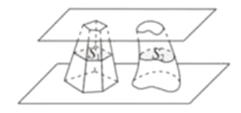
A.≥‰∑÷≤ª±ÿ“™Ãº˛B.±ÿ“™≤ª≥‰∑÷ú˛
C.≥‰∑÷±ÿ“™Ãº˛D.º»≤ª≥‰∑÷“≤≤ª±ÿ“™Ãº˛
 Ω‘ø≥◊ ‘æÌœµ¡–¥∞∏
Ω‘ø≥◊ ‘æÌœµ¡–¥∞∏
| ƒÍº∂ | ∏ş÷–øŒ≥à | ƒÍº∂ | ≥÷–øŒ≥à |
| ∏ş“ª | ∏ş“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥“ª | ≥“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏ş∂˛ | ∏ş∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥∂˛ | ≥∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏ş»˝ | ∏ş»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥»˝ | ≥»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫∏ş÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨‘Ğ’˝»˝¿‚÷˘£®µ◊√ÊŒ™’˝»˝Ω«–Œµƒ÷±¿‚÷˘£©ABC©ÅA1B1C1÷–£¨“—÷™AB£ΩAA1£Ω2£¨µ„QŒ™BCµƒ÷–µ„£Æ
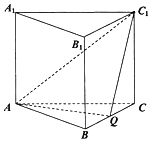
£®1£©«Û÷§£∫∆Ω√ÊAQC1°Õ∆Ω√ÊB1BCC1£ª
£®2£©«Û÷±œşCC1”Î∆Ω√ÊAQC1À˘≥…Ω«µƒ’˝«–÷µ£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏ş÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™∫Ø ˝![]() £¨»Ù∑Ω≥Ã
£¨»Ù∑Ω≥Ã![]() ”–Àƒ∏ˆ≤ªµ» µ∏˘
”–Àƒ∏ˆ≤ªµ» µ∏˘![]() £¨ ±£¨≤ªµ» Ω
£¨ ±£¨≤ªµ» Ω![]() ∫„≥…¡¢£¨‘Ú µ ˝
∫„≥…¡¢£¨‘Ú µ ˝![]() µƒ◊Ó–°÷µŒ™£®£©
µƒ◊Ó–°÷µŒ™£®£©
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏ş÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™Õ÷‘≤![]() µƒ¿Î–ƒ¬ Œ™
µƒ¿Î–ƒ¬ Œ™![]() £¨”Î
£¨”Î![]() ÷·Ωª”е„
÷·Ωª”е„![]() £¨
£¨![]() £¨π˝
£¨π˝![]() ÷·…œ“ªµ„
÷·…œ“ªµ„![]() “˝
“˝![]() ÷·µƒ¥πœş£¨ΩªÕ÷‘≤
÷·µƒ¥πœş£¨ΩªÕ÷‘≤![]() ”е„
”е„![]() £¨
£¨![]() £¨µ±
£¨µ±![]() ”ÎÕ÷‘≤”“Ωπµ„÷ÿ∫œ ±£¨
”ÎÕ÷‘≤”“Ωπµ„÷ÿ∫œ ±£¨![]() £Æ
£Æ
£®1£©«ÛÕ÷‘≤![]() µƒ∑Ω≥ãª
µƒ∑Ω≥ãª
£®2£©…Ë÷±œş![]() ”Î÷±œş
”Î÷±œş![]() Ωª”е„
Ωª”е„![]() £¨ «∑ҥʑĞ∂®µ„
£¨ «∑ҥʑĞ∂®µ„![]() ∫Õ
∫Õ![]() £¨ π
£¨ π![]() Œ™∂®÷µ£Æ»Ù¥Ê‘Ğ£¨«Û
Œ™∂®÷µ£Æ»Ù¥Ê‘Ğ£¨«Û![]() °¢
°¢![]() µ„µƒ◊¯±Í£ª»Ù≤ª¥Ê‘Ğ£¨Àµ√˜¿Ì”…£Æ
µ„µƒ◊¯±Í£ª»Ù≤ª¥Ê‘Ğ£¨Àµ√˜¿Ì”…£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏ş÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øŒ™¡À«Ï◊£÷–ª™»À√Òπ≤∫Õπ˙≥…¡¢![]() ÷݃ͣ¨ƒ≥≥µº‰ƒĞ柖–…˙≤˙±»»¸£¨”…º◊““¡Ω◊ȃĞ∏˜Àʪ˙—°»°
÷݃ͣ¨ƒ≥≥µº‰ƒĞ柖–…˙≤˙±»»¸£¨”…º◊““¡Ω◊ȃĞ∏˜Àʪ˙—°»°![]() √˚ººπ§£¨‘е•Œª ±º‰…˙≤˙Õ¨“ª÷÷¡„º˛£¨∆‰…˙≤˙µƒ∫œ∏Ò¡„º˛ ˝µƒæ•“∂Õº»Áœ¬£∫
√˚ººπ§£¨‘е•Œª ±º‰…˙≤˙Õ¨“ª÷÷¡„º˛£¨∆‰…˙≤˙µƒ∫œ∏Ò¡„º˛ ˝µƒæ•“∂Õº»Áœ¬£∫
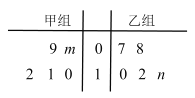
“—÷™¡Ω◊ÈÀ˘—°ººπ§…˙≤˙µƒ∫œ∏Ò¡„º˛µƒ∆Ωæ˘ ˝æ˘Œ™![]() .
.
£®1£©∑÷±«Û≥ˆ![]() µƒ÷µ£ª
µƒ÷µ£ª
£®2£©∑÷±«Û≥ˆº◊““¡Ω◊Ⱥºπ§‘е•Œª ±º‰ƒĞº”𧵃∫œ∏Ò¡„º˛µƒ∑Ω≤Ó![]() ∫Õ
∫Õ![]() ,≤¢”…¥Àπ¿º∆¡Ω◊Ⱥºπ§µƒ…˙≤˙ÀÆ∆Ω£ª
,≤¢”…¥Àπ¿º∆¡Ω◊Ⱥºπ§µƒ…˙≤˙ÀÆ∆Ω£ª
£®3£©»Ùµ•Œª ±º‰ƒĞ…˙≤˙µƒ∫œ∏Ò¡„º˛∏ˆ ˝≤ª–°”Ğ∆Ωæ˘ ˝µƒººπ§º¥Œ™°∞…˙≤˙ƒİ ÷°±£¨∏˘æı“‘…œ ˝æı£¨ƒİ∑Ò»œŒ™∏√≥µº‰50%“‘…œµƒººπ§∂º «…˙≤˙ƒİ ÷£ø
(◊¢£∫∑Ω≤Ó![]() ,∆‰÷–
,∆‰÷–![]() Œ™ ˝æı
Œ™ ˝æı![]() µƒ∆Ωæ˘ ˝).
µƒ∆Ωæ˘ ˝).
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏ş÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£®1£©Œ™ƒ≥ °2016ƒÍøϵı“µŒÒ¡øÕ≥º∆±Ì£¨Õº£®2£©ƒ≥ °2016ƒÍøϵı“µŒÒ ’»ÎÕ≥º∆±Ì£¨∂‘Õ≥º∆Õºœ¬¡–¿ÌΩ‚¥ÌŒÛµƒ «£®£©
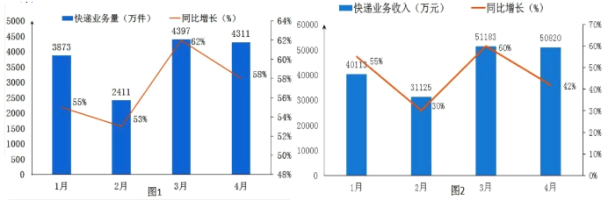
A.2016ƒÍ1°´4‘¬“µŒÒ¡ø◊Ó∏ş3‘¬◊ÓµÕ2‘¬£¨≤Ó÷µΩ”Ω¸2000ÕÚº˛
B.2016ƒÍ1°´4‘¬“µŒÒ¡øÕ¨±»‘ˆ≥§¬ æ˘≥¨π˝50£•£¨‘Ğ3‘¬◊Ó∏ş£¨∫Õ¥∫ΩĞ’ı∑¸∫ÛÕ¯π∫”≠¿¥≈Á’«”–πÿ
C.¥”¡ΩÕº÷–ø¥£¨‘ˆ¡ø”Αˆ≥§ÀŸ∂»≤¢≤ªÕÍ»´“ª÷¬£¨µ´“µŒÒ¡ø”ΓµŒÒµƒ ’»Î±‰ªØ∏ş∂»“ª÷¬
D.¥”1°´4‘¬¿¥ø¥£¨“µŒÒ¡ø”ΓµŒÒ ’»Î¡ø”–≤®∂Ø£¨µ´’˚ñ£≥÷∏şÀŸ‘ˆ≥§
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏ş÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™∫Ø ˝![]() £¨
£¨![]() £¨
£¨![]() Œ™◊‘»ª∂‘ ˝µƒµ◊ ˝£Æ
Œ™◊‘»ª∂‘ ˝µƒµ◊ ˝£Æ
£®1£©µ±![]() ±£¨≈–∂œ
±£¨≈–∂œ![]() ¡„µ„∏ˆ ˝≤¢«Û≥ˆ¡„µ„£ª
¡„µ„∏ˆ ˝≤¢«Û≥ˆ¡„µ„£ª
£®2£©»Ù∫Ø ˝![]() ¥Ê‘Ğ¡Ω∏ˆ≤ªÕ¨µƒº´÷µµ„
¥Ê‘Ğ¡Ω∏ˆ≤ªÕ¨µƒº´÷µµ„![]() £¨
£¨![]() £¨«Û µ ˝
£¨«Û µ ˝![]() µƒ»°÷µ∑∂Œß£Æ
µƒ»°÷µ∑∂Œß£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏ş÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø‘Ğ–¬∏şøº∏ƒ∏Ô÷–£¨¥Ú∆∆¡ÀŒƒ¿Ì∑÷ø∆µƒ°∞![]() °±ƒ£ Ω£¨≤ª…Ÿ °∑ı≤…”√¡À°∞
°±ƒ£ Ω£¨≤ª…Ÿ °∑ı≤…”√¡À°∞![]() °±£¨°∞
°±£¨°∞![]() °±£¨°∞
°±£¨°∞![]() °±µ»ƒ£ Ω.∆‰÷–°∞
°±µ»ƒ£ Ω.∆‰÷–°∞![]() °±ƒ£ Ωµƒ≤Ÿ◊˜”÷∏¸ ݪ∂”≠£¨º¥”Ô ˝Õ‚»˝√≈Œ™±ÿøºø∆ƒø£¨»ª∫ۑЌԿÌ∫Õ¿˙ ∑÷–—°øº“ª√≈£¨◊Ó∫Û¥” £”‡µƒÀƒ√≈÷–—°øº¡Ω√≈.ƒ≥–£Œ™¡À¡ÀΩ‚—ß…˙µƒ—°ø∆«Èøˆ£¨¥”∏ş∂˛ƒÍº∂µƒ2000√˚—ß…˙£®∆‰÷–ƒ–…˙1100»À£¨≈Æ…˙900»À£©÷–£¨≤…”√∑÷≤„≥È—˘µƒ∑Ω∑®¥”÷–≥È»°n√˚—ß…˙Ω¯––µ˜≤È.
°±ƒ£ Ωµƒ≤Ÿ◊˜”÷∏¸ ݪ∂”≠£¨º¥”Ô ˝Õ‚»˝√≈Œ™±ÿøºø∆ƒø£¨»ª∫ۑЌԿÌ∫Õ¿˙ ∑÷–—°øº“ª√≈£¨◊Ó∫Û¥” £”‡µƒÀƒ√≈÷–—°øº¡Ω√≈.ƒ≥–£Œ™¡À¡ÀΩ‚—ß…˙µƒ—°ø∆«Èøˆ£¨¥”∏ş∂˛ƒÍº∂µƒ2000√˚—ß…˙£®∆‰÷–ƒ–…˙1100»À£¨≈Æ…˙900»À£©÷–£¨≤…”√∑÷≤„≥È—˘µƒ∑Ω∑®¥”÷–≥È»°n√˚—ß…˙Ω¯––µ˜≤È.
£®1£©“—÷™≥È»°µƒn√˚—ß…˙÷–∫¨ƒ–…˙110»À£¨«Ûnµƒ÷µº∞≥È»°µΩµƒ≈Æ…˙»À ˝£ª
£®2£©‘Ğ£®1£©µƒ«Èøˆœ¬∂‘≥È»°µΩµƒn√˚Õ¨—ß°∞—°ŒÔ¿Ì°±∫Õ°∞—°¿˙ ∑°±Ω¯––Œ æ̵˜≤È£¨µ√µΩœ¬¡–2°¡2¡–¡™±Ì.«ÎΩ´¡–¡™±Ì≤π≥‰ÕÍ’˚£¨≤¢≈–∂œ «∑Ò”–99%µƒ∞—Œ’»œŒ™—°ø∆ƒø”Ζ‘±”–πÿ£ø
—°ŒÔ¿Ì | —°¿˙ ∑ | ∫œº∆ | |
ƒ–…˙ | 90 | ||
≈Æ…˙ | 30 | ||
∫œº∆ |
£®3£©‘Ğ£®2£©µƒÃº˛œ¬£¨¥”≥È»°µƒ°∞—°¿˙ ∑°±µƒ—ß…˙÷–∞¥–‘±∑÷≤„≥È—˘‘Ÿ≥È»°5√˚£¨‘Ÿ¥”’‚5√˚—ß…˙÷–≥È»°2»À¡ÀΩ‚—°’˛÷Œ°¢µÿ¿Ì°¢ªØ—ß°¢…˙ŒÔµƒ«Èøˆ£¨«Û2»À÷¡…Ÿ”–1√˚ƒ–…˙µƒ∏≈¬ .
≤Œøºπ´ Ω£∫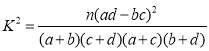 .
.
| 0.10 | 0.010 | 0.001 |
| 2.706 | 6.635 | 10.828 |
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏ş÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™∫Ø ˝f£®x£©![]() ”Îg£®x£©£Ω3elnx+mxµƒÕºœÛ”–4∏ˆ≤ªÕ¨µƒΩªµ„£¨‘Ú µ ˝mµƒ»°÷µ∑∂Œß «£® £©
”Îg£®x£©£Ω3elnx+mxµƒÕºœÛ”–4∏ˆ≤ªÕ¨µƒΩªµ„£¨‘Ú µ ˝mµƒ»°÷µ∑∂Œß «£® £©
A.£®©Å3£¨![]() £©B.£®©Å1£¨
£©B.£®©Å1£¨![]() £©C.£®©Å1£¨3£©D.£®0£¨3£©
£©C.£®©Å1£¨3£©D.£®0£¨3£©
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
∞Ÿ∂»÷¬–≈ - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒŞ÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com