
(08年辽宁卷理)设函数![]() .
.
⑴求![]() 的单调区间和极值;
的单调区间和极值;
⑵是否存在实数![]() ,使得关于
,使得关于![]() 的不等式
的不等式![]() 的解集为
的解集为![]() ?若存在,求
?若存在,求![]() 的取值范围;若不存在,试说明理由.
的取值范围;若不存在,试说明理由.
说明:本小题主要考查函数的导数,单调性,极值,不等式等基础知识,考查综合利用数学知识分析问题、解决问题的能力.满分14分.
解析:(Ⅰ)![]() .?????????????????????????? 2分
.?????????????????????????? 2分
故当![]() 时,
时,![]() ,
,
![]() 时,
时,![]() .
.
所以![]() 在
在![]() 单调递增,在
单调递增,在![]() 单调递减.??????????????????????????????????????????? 4分
单调递减.??????????????????????????????????????????? 4分
由此知![]() 在
在![]() 的极大值为
的极大值为![]() ,没有极小值.????????????????????????????? 6分
,没有极小值.????????????????????????????? 6分
(Ⅱ)()当![]() 时,
时,
由于![]() ,
,
故关于![]() 的不等式
的不等式![]() 的解集为
的解集为![]() .????????????????????????????????????????????? 10分
.????????????????????????????????????????????? 10分
()当![]() 时,由
时,由![]() 知
知![]() ,其中
,其中![]() 为正整数,且有
为正整数,且有
![]() .????????????????????????????????????? 12分
.????????????????????????????????????? 12分
又![]() 时,
时,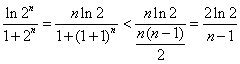 .
.
且![]() .
.
取整数![]() 满足
满足![]() ,
,![]() ,且
,且![]() ,
,
则![]() ,
,
即当![]() 时,关于
时,关于![]() 的不等式
的不等式![]() 的解集不是
的解集不是![]() .
.
综合()()知,存在![]() ,使得关于
,使得关于![]() 的不等式
的不等式![]() 的解集为
的解集为![]() ,且
,且![]() 的取值范围为
的取值范围为![]() . 14分
. 14分


 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com