
【题目】已知函数f(x)=2sinxsin(x+3φ)是奇函数,其中φ∈(0, ![]() ),则函数g(x)=cos(2x﹣φ)的图象( )
),则函数g(x)=cos(2x﹣φ)的图象( )
A.关于点( ![]() ,0)对称
,0)对称
B.可由函数f(x)的图象向右平移 ![]() 个单位得到
个单位得到
C.可由函数f(x)的图象向左平移 ![]() 个单位得到
个单位得到
D.可由函数f(x)的图象向左平移 ![]() 个单位得到
个单位得到
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案科目:高中数学 来源: 题型:
【题目】以平面直角坐标系的原点为极点,x轴的正半轴为极轴,建立极坐标系,两种坐标系中取相同的长度单位,已知曲线C1的参数方程为 ![]() ,(α为参数,且α∈[0,π)),曲线C2的极坐标方程为ρ=﹣2sinθ.
,(α为参数,且α∈[0,π)),曲线C2的极坐标方程为ρ=﹣2sinθ.
(1)求C1的极坐标方程与C2的直角坐标方程;
(2)若P是C1上任意一点,过点P的直线l交C2于点M,N,求|PM||PN|的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=x|x﹣a|+2x﹣3,其中a∈R
(1)当a=4,2≤x≤5时,求函数f(x)的最大值和最小值,并写出相应的x的值.
(2)若f(x)在R上恒为增函数,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,曲线C1的参数方程为 ![]() (a>b>0,φ为参数),以Ο为极点,x轴的正半轴为极轴建立极坐标系,曲线C2是圆心在极轴上且经过极点的圆,已知曲线C1上的点M(2,
(a>b>0,φ为参数),以Ο为极点,x轴的正半轴为极轴建立极坐标系,曲线C2是圆心在极轴上且经过极点的圆,已知曲线C1上的点M(2, ![]() )对应的参数φ=
)对应的参数φ= ![]() .θ=
.θ= ![]() 与曲线C2交于点D(
与曲线C2交于点D( ![]() ,
, ![]() ).
).
(1)求曲线C1 , C2的直角坐标方程;
(2)A(ρ1 , θ),B(ρ2 , θ+ ![]() )是曲线C1上的两点,求
)是曲线C1上的两点,求 ![]() +
+ ![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解少年儿童的肥胖是否与常喝碳酸饮料有关,现对100名五年级学生进行了问卷调查,得到如下2×2列联表,平均每天喝500ml以上为常喝,体重超过50kg为肥胖.
不常喝 | 常喝 | 合计 | |
肥胖 | x | y | 50 |
不肥胖 | 40 | 10 | 50 |
合计 | A | B | 100 |
现从这100名儿童中随机抽取1人,抽到不常喝碳酸饮料的学生的概率为 ![]()
(1)求2×2列联表中的数据x,y,A,B的值;
(2)根据列联表中的数据绘制肥胖率的条形统计图,并判断常喝碳酸饮料是否影响肥胖?
(3)是否有99.9%的把握认为肥胖与常喝碳酸饮料有关?说明你的理由. 附:参考公式:K2= ![]() ,其中n=a+b+c+d.
,其中n=a+b+c+d.
临界值表:
P(K2≥k) | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,底面ABCD是菱形,且∠ABC=120°.点E是棱PC的中点,平面ABE与棱PD交于点F. (Ⅰ)求证:AB∥EF;
(Ⅱ)若PA=PD=AD=2,且平面PAD⊥平面ABCD,求平面PAF与平面AEF所成的二面角的正弦值.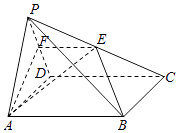
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com