
| A. | (1,2) | B. | (1,2] | C. | [2,+∞) | D. | (2,+∞) |
分析 不妨设P在双曲线右支,P点的横坐标为x,可得|PF1|=3|PF2|,利用双曲线的第二定义,可得x关于e的表达式,进而根据x的范围确定e的范围.
解答 解:∵双曲线上存在一点P,使得|PF1|,2a,|PF2|成等差数列,
∴|PF1|+|PF2|=4a,
不妨设P在双曲线右支,则|PF1|-|PF2|=2a,
∴|PF1|=3a,|PF2|=a,
∴|PF1|=3|PF2|,
设P点的横坐标为x
∵|PF1|=3|PF2|,P在双曲线右支(x≥a)
根据双曲线的第二定义,可得3e(x-$\frac{{a}^{2}}{c}$)=e(x+$\frac{{a}^{2}}{c}$)
∴ex=2a
∵x≥a,∴ex≥ea
∴2a≥ea,∴e≤2
∵e>1,∴1<e≤2
故选:B.
点评 本题主要考查等差数列的性质,考查了双曲线的简单性质,考查了双曲线的第二定义的灵活运用,属于中档题.


科目:高中数学 来源: 题型:选择题
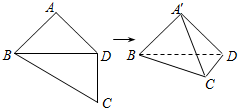 如图,在四边形ABCD中,AB=AD=CD=1,BD=$\sqrt{2}$,BD⊥CD,将四边形ABCD沿对角线BD折成四面体A′BCD,使得平面A′BD⊥平面BDC,给出下列四个结论,其中正确的有( )
如图,在四边形ABCD中,AB=AD=CD=1,BD=$\sqrt{2}$,BD⊥CD,将四边形ABCD沿对角线BD折成四面体A′BCD,使得平面A′BD⊥平面BDC,给出下列四个结论,其中正确的有( )| A. | A′B⊥CD | |
| B. | 四面体A′BCD的体积为$\frac{1}{2}$ | |
| C. | A′C与BD所成的角为60° | |
| D. | 四面体A′BCD的外接球的表面积为$\frac{7π}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
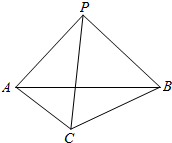 如图,在三棱锥P-ABC中,PA=PB=$\sqrt{6}$,PA⊥PB,AB⊥BC,∠BAC=30°,平面PAB⊥平面ABC.
如图,在三棱锥P-ABC中,PA=PB=$\sqrt{6}$,PA⊥PB,AB⊥BC,∠BAC=30°,平面PAB⊥平面ABC.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 20$\sqrt{2}$ | B. | 20 | C. | 20$\sqrt{3}$ | D. | 10$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com