Question

（09年临沂一模理）（12分）

如图，在直棱柱ABC-A₁B₁C₁中，AC=BC=AA₁,∠ACB＝90º，G为BB₁的中点。

(1)求证：平面A₁CG⊥平面A₁GC₁;

(2)求平面ABC与平面A₁GC所成锐二面角的平面角的余弦值。

Answer 1

解析：（I）证明：在直棱柱ABC-A₁B₁C₁中，有A₁C₁⊥CC_1。

     ∵ ∠ACB＝90º，∴A₁C₁⊥C₁B₁，即A₁C₁⊥平面C₁CBB₁，

   ∵CG平面C₁CBB₁,∴A₁C₁⊥CG。┉┉┉┉┉┉┉┉2分

   在矩形C₁CBB₁中，CC₁＝BB₁＝2BC，G为BB₁的中点，

   CG＝BC，C₁G＝BC，CC₁＝2BC

   ∴∠CGC₁＝90，即CG⊥C₁G┉┉┉┉┉┉┉┉4分

而A₁C₁∩C₁G=C₁，

∴CG⊥平面A₁GC₁。

∴平面A₁CG⊥平面A₁GC₁。┉┉┉┉┉┉┉┉6分

（II）由于CC₁平面ABC，

 ∠ACB＝90º，建立如图所示的空间坐标系，设AC＝BC＝CC₁＝a，则A(a,0,0),B(0,a,0)

A₁(a,0,2a),G(0,a,a).

∴=(a,0,2a),=(0,a,a). ┉┉┉┉┉┉┉┉8分

设平面A₁CG的法向量n₁=(x₁,y₁,z₁),

由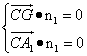得

令z₁=1,n₁=(-2,-1,1). ┉┉┉┉┉┉┉┉9分

又平面ABC的法向量为n₂=(0,0,1) ┉┉┉┉┉┉┉┉10分

设平面ABC与平面A₁CG所成锐二面角的平面角为θ，

则┉┉┉┉┉┉┉┉11分

即平面ABC与平面A₁CG所成锐二面角的平面角的余弦值为。┉┉┉12分