
���� ��1�������Ҷ����ɵ�b=$\frac{\sqrt{3}}{sin\frac{��}{4}}$$•\frac{3}{5}$=$\frac{3\sqrt{6}}{5}$�����Ҷ����ɵ�3=c2+$\frac{54}{25}$-2•$\frac{3\sqrt{6}}{5}$c•$\frac{\sqrt{2}}{2}$���������c��
��2�������Ҷ����ɵ�$\left\{\begin{array}{l}{3={b}^{2}+{c}^{2}-\sqrt{2}bc}\\{��\frac{\sqrt{6}}{2}��^{2}={b}^{2}+\frac{{c}^{2}}{4}-\frac{\sqrt{2}}{2}bc}\end{array}\right.$�����b��������$\overrightarrow{CA}$•$\overrightarrow{CB}$��ֵ��
��� �⣺��1�������Ҷ����ɵ�b=$\frac{\sqrt{3}}{sin\frac{��}{4}}$$•\frac{3}{5}$=$\frac{3\sqrt{6}}{5}$
�����Ҷ����ɵ�3=c2+$\frac{54}{25}$-2•$\frac{3\sqrt{6}}{5}$c•$\frac{\sqrt{2}}{2}$��
��c2-$\frac{6\sqrt{3}}{5}$c-$\frac{21}{25}$=0��
��c=$\frac{7\sqrt{3}}{5}$��
��2�������Ҷ����ɵ�$\left\{\begin{array}{l}{3={b}^{2}+{c}^{2}-\sqrt{2}bc}\\{��\frac{\sqrt{6}}{2}��^{2}={b}^{2}+\frac{{c}^{2}}{4}-\frac{\sqrt{2}}{2}bc}\end{array}\right.$����b=$\sqrt{3}$��
��|$\overrightarrow{CA}$+$\overrightarrow{CB}$|=$\sqrt{6}$��
��3+3+2$\overrightarrow{CA}$•$\overrightarrow{CB}$=6��
��$\overrightarrow{CA}$•$\overrightarrow{CB}$=0��
���� ���⿼�����Ҷ��������Ҷ��������ã�����ѧ�������������������������е��⣮


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
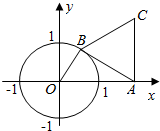 ��ͼ��ƽ��ֱ������ϵ�У�OΪ����ԭ�㣬��B�ڵ�λԲ�ϣ�A��2��0������AOB=�ȣ���ABCΪ�ȱ������Σ�
��ͼ��ƽ��ֱ������ϵ�У�OΪ����ԭ�㣬��B�ڵ�λԲ�ϣ�A��2��0������AOB=�ȣ���ABCΪ�ȱ������Σ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\overrightarrow{a}$��$\overrightarrow{b}$���ߣ�$\overrightarrow{b}$��$\overrightarrow{c}$���ߣ���$\overrightarrow{a}$��$\overrightarrow{c}$Ҳ���� | |
| B�� | ����������ȵķ���������ʼ�����յ�����һƽ���ı��ε��ĸ����� | |
| C�� | ����$\overrightarrow{a}$��$\overrightarrow{b}$�����ߣ���$\overrightarrow{a}$��$\overrightarrow{b}$���Ƿ������� | |
| D�� | ����ͬ������������������ƽ�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com