解:(1)y=2x+1与其反函数
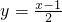
的交点坐标为(-1,-1);…(1分)
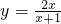
与其反函数
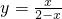
的交点坐标为(0,0),(1,1);…(3分)
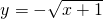
与其反函数y=x
2-1(x≤0)的交点坐标为

.…(6分)
(2)原函数图象与其反函数图象的交点关于直线y=x对称,但不一定在直线y=x上. …(10分)
(3)设点(a,b)是f(x)的图象与其反函数图象的任一交点,由于原函数与反函数图象关于直线y=x对称,
则点(b,a)也是f(x)的图象与其反函数图象的交点,且有b=f(a),a=f(b).…(12分)
①若a=b,交点显然在直线y=x上.…(13分)
②若a<b且f(x)是增函数时,有f(b)<f(a),从而有b<a,与a<b矛盾;若b<a且f(x)是增函数
时,有f(a)<f(b),从而有a<b,与b<a矛盾.…(15分)
③若a<b且f(x)是减函数时,有f(b)<f(a),从而有a<b成立,此时交点不在直线y=x上;
同理,若b<a且f(x)是减函数时,交点也不在直线y=x上.…(17分)
综上,若函数f(x)是增函数,且f(x)的图象与其反函数的图象有交点,则交点一定在直线y=x上;若
函数f(x)是减函数,且f(x)的图象与其反函数的图象有交点,则交点不一定在直线y=x上. (18分)
分析:(1)分别求出函数y=2x+1,
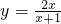
,
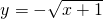
的反函数,然后求出与对应函数的交点坐标即可;
(2)根据交点坐标观察发现原函数图象与其反函数图象的交点关于直线y=x对称,但不一定在直线y=x上;
(3)设点(a,b)是f(x)的图象与其反函数图象的任一交点,由于原函数与反函数图象关于直线y=x对称,则点(b,a)也是f(x)的图象与其反函数图象的交点,讨论a、b的大小和函数的单调性可得结论.
点评:本小题主要考查反函数,互为反函数图象的交点等基础知识,考查运算求解能力,考查数形结合思想,属于中档题.

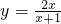 ,
,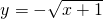 ,分别求出以上函数与其反函数图象的交点坐标;
,分别求出以上函数与其反函数图象的交点坐标;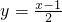 的交点坐标为(-1,-1);…(1分)
的交点坐标为(-1,-1);…(1分)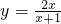 与其反函数
与其反函数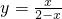 的交点坐标为(0,0),(1,1);…(3分)
的交点坐标为(0,0),(1,1);…(3分)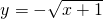 与其反函数y=x2-1(x≤0)的交点坐标为
与其反函数y=x2-1(x≤0)的交点坐标为 .…(6分)
.…(6分)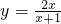 ,
,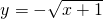 的反函数,然后求出与对应函数的交点坐标即可;
的反函数,然后求出与对应函数的交点坐标即可;

![]() ,
,![]() ,分别求出以上函数与其反函数图象的交点坐标;
,分别求出以上函数与其反函数图象的交点坐标;