
【题目】已知椭圆![]() 及以下3个函数:①
及以下3个函数:①![]() ;②
;②![]() ;③
;③![]() ,其中函数图象能等分该椭圆面积的函数个数有( )
,其中函数图象能等分该椭圆面积的函数个数有( )
A.0个B.1个C.2个D.3个
【答案】C
【解析】
由椭圆的几何性质可得椭圆![]() 的图像关于原点对称,因为函数
的图像关于原点对称,因为函数![]() ,函数
,函数![]() 为奇函数,其图像关于原点对称,则①②满足题意, 对于函数
为奇函数,其图像关于原点对称,则①②满足题意, 对于函数![]() 在
在![]() 轴右侧
轴右侧![]() 时,
时,![]() ,只有
,只有![]() 时,
时,![]() ,即函数
,即函数![]() 在
在![]() 轴右侧的图像显然不能等分椭圆在
轴右侧的图像显然不能等分椭圆在![]() 轴右侧的图像的面积,又函数
轴右侧的图像的面积,又函数![]() 为偶函数, 其图像关于
为偶函数, 其图像关于![]() 轴对称,则函数
轴对称,则函数![]() 在
在![]() 轴左侧的图像显然也不能等分椭圆在
轴左侧的图像显然也不能等分椭圆在![]() 轴左侧的图像的面积,即函数
轴左侧的图像的面积,即函数![]() 的图像不能等分该椭圆面积,得解.
的图像不能等分该椭圆面积,得解.
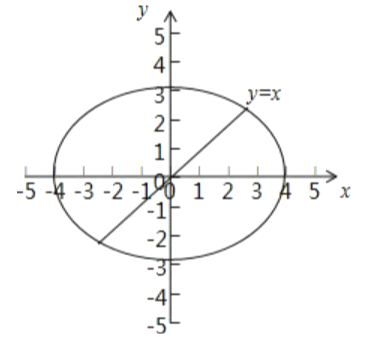
解:因为椭圆![]() 的图像关于原点对称,
的图像关于原点对称,
对于①,函数![]() 为奇函数,其图像关于原点对称,即可知
为奇函数,其图像关于原点对称,即可知![]() 的图象能等分该椭圆面积;
的图象能等分该椭圆面积;
对于②,函数![]() 为奇函数,其图像关于原点对称,即可知
为奇函数,其图像关于原点对称,即可知![]() 的图象能等分该椭圆面积;
的图象能等分该椭圆面积;
对于③,对于函数![]() 在
在![]() 轴右侧
轴右侧![]() 时,
时,![]() ,只有
,只有![]() 时,
时,![]() ,即函数
,即函数![]() 在
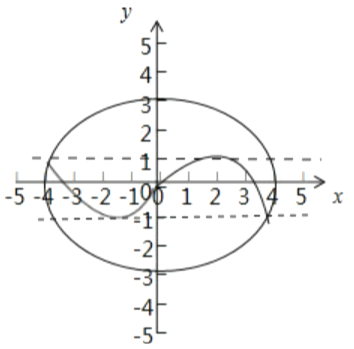
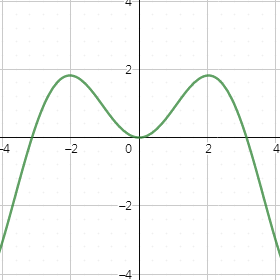
在![]() 轴右侧的图像(如图)显然不能等分椭圆在
轴右侧的图像(如图)显然不能等分椭圆在![]() 轴右侧的图像的面积,又函数
轴右侧的图像的面积,又函数![]() 为偶函数, 其图像关于
为偶函数, 其图像关于![]() 轴对称,则函数
轴对称,则函数![]() 在
在![]() 轴左侧的图像显然也不能等分椭圆在
轴左侧的图像显然也不能等分椭圆在![]() 轴左侧的图像的面积,即函数
轴左侧的图像的面积,即函数![]() 的图像不能等分该椭圆面积,
的图像不能等分该椭圆面积,
即函数图象能等分该椭圆面积的函数个数有2个,
故选:C.


科目:高中数学 来源: 题型:
【题目】某手机企业为确定下一年度投入某种产品的研发费用,统计了近![]() 年投入的年研发费用
年投入的年研发费用![]() 千万元与年销售量
千万元与年销售量![]() 千万件的数据,得到散点图1,对数据作出如下处理:令
千万件的数据,得到散点图1,对数据作出如下处理:令![]() ,
,![]() ,得到相关统计量的值如图2:
,得到相关统计量的值如图2:

(1)利用散点图判断![]() 和
和![]()
![]() 哪一个更适合作为年研发费用
哪一个更适合作为年研发费用![]() 和年销售量
和年销售量![]() 的回归类型(不必说明理由),并根据数据,求出
的回归类型(不必说明理由),并根据数据,求出![]() 与
与![]() 的回归方程;
的回归方程;
(2)已知企业年利润![]() 千万元与
千万元与![]() 的关系式为
的关系式为![]() (其中
(其中![]() 为自然对数的底数),根据(1)的结果,要使得该企业下一年的年利润最大,预计下一年应投入多少研发费用?
为自然对数的底数),根据(1)的结果,要使得该企业下一年的年利润最大,预计下一年应投入多少研发费用?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司的新能源产品上市后在国内外同时销售,已知第一批产品上市销售40天内全部售完,该公司对这批产品上市后的国内外市场销售情况进行了跟踪调查,如图所示,其中图①中的折线表示的是国外市场的日销售量与上市时间的关系;图②中的抛物线表示的是国内市场的日销售量与上市时间的关系;下表表示的是产品广告费用、产品成本、产品销售价格与上市时间的关系.
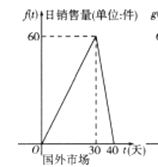 图① 图②
图① 图②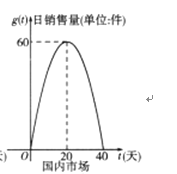
第t天产品广告费用(单位:万元) | 每件产品成本(单位:万元) | 每件产品销售价格(单位:万元) | |
|
| 3 | 6 |
| 10 | 3 | 5 |
(1)分别写出国外市场的日销售量![]() 、国内市场的日销售量
、国内市场的日销售量![]() 与产品上市时间t的函数关系式;
与产品上市时间t的函数关系式;
(2)产品上市后的哪几天,这家公司的日销售利润超过260万元?
(日销售利润=(单件产品销售价-单件产品成本)×日销售量-当天广告费用,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】经过市场调查,某种商品在销售中有如下关系:第x(![]() )天的销售价格(单位:元/件)为
)天的销售价格(单位:元/件)为![]() ,第x天的销售量(单位:件)为
,第x天的销售量(单位:件)为![]() (
(![]() 为常数),且在第20天该商品的销售收入为600元(销售收入=销售价格×销售量).
为常数),且在第20天该商品的销售收入为600元(销售收入=销售价格×销售量).
(1)求a的值,并求第15天该商品的销售收入;
(2)求在这30天中,该商品日销售收入y的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的定义域为
的定义域为![]() ,部分对应值如下表.
,部分对应值如下表.
x |
| 0 | 4 | 5 |
| 1 | 2 | 2 | 1 |
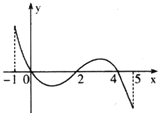
![]() 的导函数
的导函数![]() 的图象如图所示:下列关于
的图象如图所示:下列关于![]() 的命题:
的命题:
![]() 函数
函数![]() 是周期函数;
是周期函数;
![]() 函数
函数![]() 在
在![]() 是减函数;
是减函数;
![]() 如果当
如果当![]() 时,
时,![]() 的最大值是2,那么t的最大值为4;
的最大值是2,那么t的最大值为4;
![]() 函数
函数![]() 的零点个数可能为0、1、2、3、4个.
的零点个数可能为0、1、2、3、4个.
其中正确命题的序号是______.
查看答案和解析>>
科目:高中数学 来源: 题型:
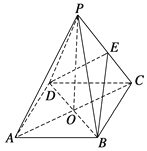
【题目】如图所示,ABCD是正方形,O是正方形的中心,PO⊥底面ABCD,底面边长为a,E是PC的中点.
(1)求证:平面PAC⊥平面BDE;
(2)若二面角E-BD-C为30°,求四棱锥P-ABCD的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】暑假期间,某旅行社为吸引游客去某风景区旅游,推出如下收费标准:若旅行团人数不超过30,则每位游客需交费用600元;若旅行团人数超过30,则游客每多1人,每人交费额减少10元,直到达到70人为止.
(1)写出旅行团每人需交费用![]() (单位:元)与旅行团人数
(单位:元)与旅行团人数![]() 之间的函数关系式;
之间的函数关系式;
(2)旅行团人数为多少时,旅行社可以从该旅行团获得最大收入?最大收入是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知一家公司生产某种品牌服装的年固定成本为10万元,每生产1千件需另投入2.7万元.设该公司一年内共生产该品牌服装x千件并全部销售完,每千件的销售收入为![]() 万元,且
万元,且 .
.
(1)写出年利润W(万元)关于年产量x(千件)的函数解析式;
(2)年产量为多少千件时,该公司在这一品牌服装的生产中所获得利润最大?(注:年利润=年销售收入﹣年总成本)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() 过点
过点![]() ,且与
,且与![]() 轴、
轴、![]() 轴都交于正半轴,当直线
轴都交于正半轴,当直线![]() 与坐标轴围成的三角形面积取得最小值时,求:
与坐标轴围成的三角形面积取得最小值时,求:
(1)直线![]() 的方程;
的方程;
(2)直线l关于直线m:y=2x-1对称的直线方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com