
 是[-1,0]上的一阶回归函数
是[-1,0]上的一阶回归函数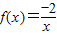 是(0,+∞)上的二阶回归函数;
是(0,+∞)上的二阶回归函数; 是(2,+∞)上的三阶回归函数.
是(2,+∞)上的三阶回归函数.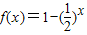 在[-1,0]上,是否满足定义可判断①②的真假;根据二阶回归函数的概念,判断
在[-1,0]上,是否满足定义可判断①②的真假;根据二阶回归函数的概念,判断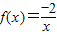 在(0,+∞)上是否满足定义可判断③的真假;根据三阶回归函数的概念,判断
在(0,+∞)上是否满足定义可判断③的真假;根据三阶回归函数的概念,判断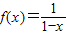 在(2,+∞)上是否满足定义可判断④的真假;
在(2,+∞)上是否满足定义可判断④的真假;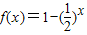 在[-1,0]上单调递增,∴当x=-1时,f(x)取最小值-1,当x=0时,f(x)取最大值0,
在[-1,0]上单调递增,∴当x=-1时,f(x)取最小值-1,当x=0时,f(x)取最大值0,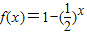 ,x∈[-1,0]}=[-1,0],故②中函数是一阶回归函数,故②正确;
,x∈[-1,0]}=[-1,0],故②中函数是一阶回归函数,故②正确;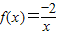 ,∴x∈(0,+∞)时,y=f(f(x))=
,∴x∈(0,+∞)时,y=f(f(x))=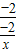 =x∈(0,+∞),即③中函数是二阶回归函数,故③正确;
=x∈(0,+∞),即③中函数是二阶回归函数,故③正确;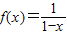 ,∴x∈(2,+∞)时,y=f(f(f(x)))=
,∴x∈(2,+∞)时,y=f(f(f(x)))=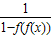 =
=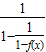 =
=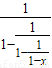 =
=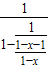 =
=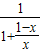 =
=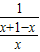 =x∈(2,+∞),即④中函数是三阶回归函数,故④正确;
=x∈(2,+∞),即④中函数是三阶回归函数,故④正确;

科目:高中数学 来源: 题型:
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| k |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 2 |
| -2 |
| x |
| 1 |
| 1-x |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

 .请结合(I)中的结论证明x1<x3<x2.
.请结合(I)中的结论证明x1<x3<x2.查看答案和解析>>
科目:高中数学 来源:2002-2013学年江苏省泰州二中高二(下)期中数学试卷(理科)(解析版) 题型:解答题

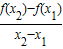 .请结合(I)中的结论证明x1<x3<x2.
.请结合(I)中的结论证明x1<x3<x2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com