【题目】已知函数
.
(1)求该函数的最小正周期和最小值;
(2)若
,求该函数的单调递增区间.
【答案】（1）
；（2）
，
.
【解析】
(1)将函数解析式第二项利用二倍角的正弦函数公式化简,第一、三项利用平方差公式分解因式后利用同角三角 函数间的基本关系及二倍角的余弦函数公式化简,再利用两角和与差的正弦函数公式及特殊角的三角函数值化为一个角的正弦函数,找出
的值,代入周期公式
,即可求出函数的最小正周期;由正弦函数的值域得出函数的值域,即可确定出函数的最小值;(2)由正弦函数的单调增区间
,列出关于x的不等式,求出不等式的解集,令解集中
和1,得到x的范围,与
取交集,即可得到该函数的单调递增区间.
(1)
,
,
又
,
则
;
(2)令
，
,
则
令,1,得到
或
,
与取交集,得到
或
,
则当时,函数的递增区间是和
科目：高中数学 来源： 题型：
【题目】已知集合M是满足下列性质的函数f（x）的全体：存在非零常数T，对任意x∈R，有f（x+T）=Tf（x）成立．
（1）函数f（x）=x是否属于集合M？说明理由；
（2）设函数f（x）=ax（a＞0，且a≠1）的图象与y=x的图象有公共点，证明：f（x）=ax∈M；
（3）若函数f（x）=sinkx∈M，求实数k的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在平面直角坐标系xOy中，曲线C的参数方程为
（
为参数），以坐标原点为极点，x轴的正半轴为极轴建立极坐标系，直线l的极坐标方程为
.
（1）求曲线C的极坐标方程和直线l的直角坐标方程；
（2）若射线
与曲线C交于点A（不同于极点O），与直线l交于点B，求
的最大值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某单位一辆交通车载有8个职工从单位出发送他们下班回家，途中共有甲、乙、丙3个停车点．如果某停车点无人下车，那么该车在这个点就不停车．假设每个职工在每个停车点下车的可能性都是相等的，求下列事件的概率：
（1）该车在某停车点停车；
（2）停车的次数不少于2次；
（3）恰好停车2次．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如果执行程序框图，输入正整数
，
，满足
，那么输出的
等于（ ）．
[Failed to download image : http://192.168.0.10:8086/QBM/2020/6/25/2492401463009280/2492946029182977/STEM/3a3c20c7c34c41528daf48813411739a.png]
A.
B.
C.
D.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】甲、乙、丙三台机床各自独立地加工同一种零件，已知甲机床加工的零件是一等品而乙机床加工的零件不是一等品的概率为
，乙机床加工的零件是一等品而丙机床加工的零件不是一等品的概率为
，甲、丙两台机床加工的零件都是一等品的概率为
．
（1）分别求甲、乙、丙三台机床各自加工的零件是一等品的概率；
（2）从甲、乙、丙加工的零件中各取一个检验，求至少有一个一等品的概率．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图所示，正四棱锥
底面的四个顶点
，
，
，
在球
的同一个大圆上，点
在球面上，且已知
．
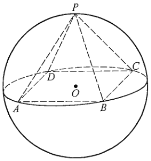
（1）求球的表面积；
（2）设
为
中点，求异面直线
与
所成角的大小．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】观察不等式：
，
，
，
，
由此归纳第
个不等式为____________；要用数学归纳法证明该不等式，由
时不等式成立，推证
时，左边应增加的项数为____________.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知数列
的首项
（
是常数，且
），
，数列
的首项
，
．
（1）证明：从第2项起是以2为公比的等比数列；
（2）设
为数列的前
项和，且
是等比数列，求实数的值；
（3）当
时，求数列的最小项．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com