练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    若椭圆C1：
    x2
    a2
    +
    y2
    b2
    =1    （a＞b＞0）过点（2，1），离心率为
    		2
    2
    ，F1，F2分别为其左、右焦点．
    （Ⅰ）若点P与F1，F2的距离之比为
    1
    3
    ，求直线x-
    		2
    y+
    		3
    =0    被点P所在的曲线C2截得的弦长；
    （Ⅱ） 设A1，A2分别为椭圆C1的左、右顶点，Q为C1上异于A1，A2的任意一点，直线A1Q交C1的右准线于点M，直线A2Q交C1的右准线于点N，求证MF2⊥NF2．
    由题意得：
    22
    a2
    +
    12
    b2
    =1
    c
    a
    =
    		2
    2
    ?
    a=
    		6
    b=
    		3
    c=
    		3
    ，F1，F2的坐标分别为：（-
    		3
    ，0），（
    		3
    ，0）．
    （I）设点P（x，y）与F1，F2的距离之比为
    1
    3
    ，
    则：
    		(x+
    		3
    ) 2+y 2
    		(x-
    		3
    ) 2+y 2 
    =
    1
    3
    ?（x+
    3
    		3
    4
    ）2+y2=
    27
    16
    ，
    是一个圆心在（-
    3
    		3
    4
    ，0）半径为：
    3
    		3
    4
    的圆，
    圆心到直线直线x-
    		2
    y+
    		3
    =0    的距离为d=
    		3
    4
    		3
    =
    1
    4
    ，
    直线x-
    		2
    y+
    		3
    =0    被点P所在的曲线C2截得的弦长为：
    2
    27
    16
    -
    1
    16
    =
    		26
    2
    ．
    （II）设Q（s，t），由题意直线QA1的方程为
    y
    t
    +
    x-
    		6
    s+
    		6
    =1    ，
    直线QA2的方程为
    y
    t
    +
    x+
    		6
    s-
    		6
    =1    ，
    由于椭圆右准线方程为x=
    a2
    c
    =2
    		3
    ，F2（
    		3
    ，0），
    ∵直线QA1．QA2分别交椭圆的右准线于M、N点
    ∴M（2，
    6
    s+
    		6
    t    ），N（2，
    2
    s-
    		6
    t    ）
    又P（s，t）在椭圆上，故有t2=3-
    s2
    2
     代入整理得
    kMF 2•k NF 2=-1
    ∴MF2⊥NF2．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知椭圆C1：
    x2
    a2
    +
    y2
    b2
    =1    （a＞b＞0）与双曲线 C2：x2-
    y2
    4
    =1    有公共的焦点，C2的一条渐近线与以C1的长轴为直径的圆相交于A，B两点，若C1恰好将线段AB三等分，则椭圆C1的离心率为 （　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

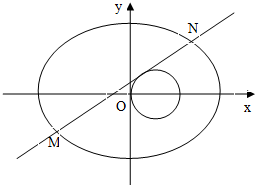
    已知椭圆C1：
    x2
    a2
    +
    y2
    b2
    =1(a＞b＞0)    过点(2，
    		3
    )    ，且它的离心率e=
    1
    2
    ．直线l：y=kx+t与椭圆C1交于M、N两点．
    （Ⅰ）求椭圆的标准方程；
    （Ⅱ）当k=
    		3
    2
    时，求证：M、N两点的横坐标的平方和为定值；
    （Ⅲ）若直线l与圆C2：(x-1)2+y2=1相切，椭圆上一点P满足
    OM
    +
    ON
    =λ
    OP
    ，求实数λ的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    若椭圆C1：
    x2
    a2
    +
    y2
    b2
    =1    （a＞b＞0）过点（2，1），离心率为
    		2
    2
    ，F1，F2分别为其左、右焦点．
    （Ⅰ）若点P与F1，F2的距离之比为
    1
    3
    ，求直线x-
    		2
    y+
    		3
    =0    被点P所在的曲线C2截得的弦长；
    （Ⅱ） 设A1，A2分别为椭圆C1的左、右顶点，Q为C1上异于A1，A2的任意一点，直线A1Q交C1的右准线于点M，直线A2Q交C1的右准线于点N，求证MF2⊥NF2．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

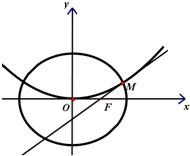
    椭圆C1：
    x2
    a2
    +
    y2
    b2
    =1(a＞b＞0)    与抛物线C2：x2=2py（p＞0）的一个交点为M，抛物线C2在点M处的切线过椭圆C1的右焦点F．
    （Ⅰ）若M(2，
    2
    		5
    5
    )    ，求C1和C2的标准方程；
    （II）求椭圆C1离心率的取值范围．

    查看答案和解析>>

    同步练习册答案