
分析 求出椭圆$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1和双曲线$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{12}$=1的离心率.利用韦达定理,可得结论.
解答 解:椭圆$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1的离心率为$\frac{1}{2}$,双曲线$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{12}$=1的离心率为2,
∴2+$\frac{1}{2}$=$\frac{5}{2}$,2×$\frac{1}{2}$=1,
∴以椭圆$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1和双曲线$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{12}$=1的离心率为根的方程为x2-$\frac{5}{2}$x+1=0.
故答案为:x2-$\frac{5}{2}$x+1=0.
点评 本题以椭圆$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1和双曲线$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{12}$=1的离心率为载体,考查一元二次方程,考查学生的计算能力,正确求出椭圆$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1和双曲线$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{12}$=1的离心率是关键.


 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:高中数学 来源: 题型:填空题
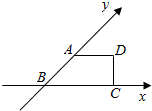 一个水平放置的平面图形的斜二测直观图是直角梯形ABCD,如图所示,∠ABC=45°,$AB=AD=\sqrt{2}$,DC⊥BC,这个平面图形的面积为$4+\sqrt{2}$.
一个水平放置的平面图形的斜二测直观图是直角梯形ABCD,如图所示,∠ABC=45°,$AB=AD=\sqrt{2}$,DC⊥BC,这个平面图形的面积为$4+\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3个 | B. | 2个 | C. | 1个 | D. | 无数个 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)是周期函数 | B. | f(x)的对称轴方程为x=$\frac{kπ}{4}$,k∈Z | ||
| C. | f(x)在区间($\frac{π}{4}$,$\frac{3π}{4}$)上为增函数 | D. | 方程f(x)=$\frac{6}{5}$在区间[-$\frac{3}{2}$π,0]上有6个根 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
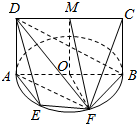 如图所示,矩形ABCD所在的平面垂直圆O所在的平面,AB是圆O的直径,M是CD上一点,且DM=EF,E、F是圆O上的点,∠EAF=∠FAB=30°.
如图所示,矩形ABCD所在的平面垂直圆O所在的平面,AB是圆O的直径,M是CD上一点,且DM=EF,E、F是圆O上的点,∠EAF=∠FAB=30°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com