Question

【题目】如图是为求S=1+ + +… 的和而设计的程序框图，将空白处补上，指明它是循环结构中的哪一种类型，并画出它的另一种循环结构框图．如图是当型循环结构．

Answer 1

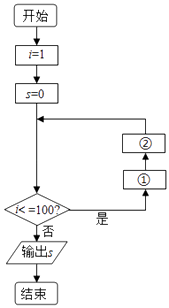
【答案】解：程序的功能是求S=1+ + +… 的值，且在循环体中，计数变量i=i+1，
故累加变量S=S+ 表示，每次累加的是 的值，
从而
① ，
②i=i+1，
③当型循环结构
它的另一种循环结构框图如右图所示：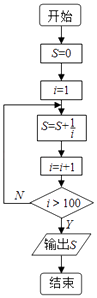

【解析】根据已知中程序的功能是求S=1+ + +… 的值，这是一个累加求和问题，共100项相加，可设计一个计数变量，一个累加变量，用循环结构实现这一算法，进而得到答案．
【考点精析】解答此题的关键在于理解程序框图的相关知识，掌握程序框图又称流程图，是一种用规定的图形、指向线及文字说明来准确、直观地表示算法的图形;一个程序框图包括以下几部分：表示相应操作的程序框；带箭头的流程线；程序框外必要文字说明．