
【题目】已知函数f(x)=ex(2x﹣1),g(x)=ax﹣a(a∈R).
(1)若y=g(x)为曲线y=f(x)的一条切线,求a的值;
(2)已知a<1,若存在唯一的整数x0 , 使得f(x0)<g(x0),求a的取值范围.
【答案】
(1)解:f′(x)=ex(2x﹣1)+2ex=ex(2x+1),
设切点为(m,n),由题意可得a=em(2m+1),
又n=am﹣a=em(2m﹣1),
解方程可得,a=1或4 ![]()
(2)解:函数f(x)=ex(2x﹣1),g(x)=ax﹣a
由题意知存在唯一的整数x0使得f(x0)在直线y=ax﹣a的下方,
∵f′(x)=ex(2x﹣1)+2ex=ex(2x+1),
∴当x<﹣ ![]() 时,f′(x)<0,
时,f′(x)<0,
当x>﹣ ![]() 时,f′(x)>0,
时,f′(x)>0,
∴当x=﹣ ![]() 时,f(x)取最小值﹣2
时,f(x)取最小值﹣2 ![]() ,
,
当x=0时,f(0)=﹣1,当x=1时,f(1)=e>0,
直线y=ax﹣a恒过定点(1,0)且斜率为a,
故﹣a>f(0)=﹣1且f(﹣1)=﹣3e﹣1≥﹣a﹣a,
解得 ![]() ≤a<1.
≤a<1.
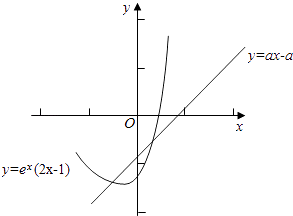
【解析】(1)求出导数,设出切点(m,n),求得切线的斜率,由切线的方程,可得a=em(2m+1),又n=am﹣a=em(2m﹣1),解方程可得a的值;(2)函数f(x)=ex(2x﹣1),g(x)=kx﹣k,问题转化为存在唯一的整数x0使得f(x0)在直线y=kx﹣k的下方,求导数可得函数的极值,数形结合可得﹣k>f(0)=﹣1且f(﹣1)=﹣3e﹣1≥﹣k﹣k,解关于k的不等式组可得.


科目:高中数学 来源: 题型:
【题目】某公司为激励创新,计划逐年加大研发资金投入,若该公司2015年全年投入研发资金超过130万元,在此基础上,每年投入的研发资金比上一年增长12%,则该公司全年投入的研发资金开始超过200万元的年份是年.(参考数据:lg1.12≈0.05,lg1.3≈0.11,lg2≈0.30).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=1+x﹣ ![]() +
+ ![]() ﹣
﹣ ![]() +…+
+…+ ![]() ;g(x)=1﹣x+
;g(x)=1﹣x+ ![]() ﹣
﹣ ![]() +
+ ![]() ﹣…﹣
﹣…﹣ ![]() ;设函数F(x)=[f(x+3)]2015[g(x﹣4)]2016 , 且函数F(x)的零点均在区间[a,b](a<b,a,b∈Z)内,则b﹣a的最小值为( )
;设函数F(x)=[f(x+3)]2015[g(x﹣4)]2016 , 且函数F(x)的零点均在区间[a,b](a<b,a,b∈Z)内,则b﹣a的最小值为( )
A.8
B.9
C.10
D.11
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a>0,a≠1且loga3>loga2,若函数f(x)=logax在区间[a,2a]上的最大值与最小值之差为1.
(1)求a的值;
(2)解不等式 ![]() ;
;
(3)求函数g(x)=|logax﹣1|的单调区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)是定义在R上的函数,满足f(x)=f(4﹣x),且对任意x1 , x2∈(0,+∞),都有(x1﹣x2)[f(x1+2)﹣f(x2+2)]>0,则满足f(2﹣x)=f( ![]() )的所有x的和为( )
)的所有x的和为( )
A.﹣3
B.﹣5
C.﹣8
D.8
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某校高一年级1000名学生中随机抽取100名测量身高,测量后发现被抽取的学生身高全部介于155厘米到195厘米之间,将测量结果分为八组:第一组[155,160),第二组[160,165),…,第八组[190,195),得到频率分布直方图如图所示. (Ⅰ)计算第三组的样本数;并估计该校高一年级1000名学生中身高在170厘米以下的人数;
(Ⅱ)估计被随机抽取的这100名学生身高的中位数、平均数.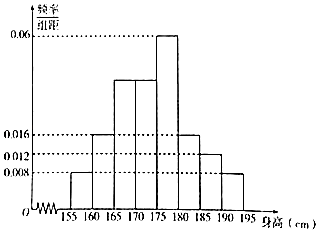
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C:y2=2px(p>0)的焦点为F,A为C上异于原点的任意一点,过点A的直线l交C于另一点B,交x轴的正半轴交于点D,且有|FA|=|FD|,当点A的横坐标为3时,△ADF为正三角形
(1)求C的方程
(2)延长AF交抛物线于点E,过点E作抛物线的切线l1 , 求证:l1∥l.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() ,且该函数的图象过点(1,5). (Ⅰ)求f(x)的解析式,并判断f(x)的奇偶性;
,且该函数的图象过点(1,5). (Ⅰ)求f(x)的解析式,并判断f(x)的奇偶性;
(Ⅱ)判断f(x)在区间(0,2)上的单调性,并用函数单调性的定义证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com