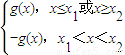【答案】
分析:(1)记g(x)=e
x-bx,当b=1时,g′(x)=e
x-1,从而可得f′(1)=g′(1)=e-1,由此可求切线方程;
(2)f(x)=0同解于g(x)=0,因此,只需g(x)=0有且只有一个解,即方程e
x-bx=0有且只有一个解,因为x=0不满足方程,所以方程同解于b=
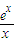
,分类讨论可得当x∈(0,+∞)时,方程有且只有一解等价于b=e;当x∈(-∞,0)时,方程有且只有一解等价于b∈(-∞,0),从而可得b的取值范围;
(3)由g′(x)=e
x-b=0,得x=lnb,从而可得在x=lnb时,g(x)取极小值g(lnb)=b-blnb=b(1-lnb),再分类讨论,即可得到结论.
解答:解:(1)记g(x)=e
x-bx.
当b=1时,g′(x)=e
x-1.
当x>0时,g′(x)>0,所以g(x)在(0,+∞)上为增函数.
又g(0)=1>0,所以当x∈(0,+∞)时,g(x)>0.
所以当x∈(0,+∞)时,f(x)=|g(x)|=g(x),
所以f′(1)=g′(1)=e-1.
所以曲线y=f(x)在点(1,e-1)处的切线方程为:y-(e-1)=(e-1)(x-1),即y=(e-1)x. …(4分)
(2)f(x)=0同解于g(x)=0,因此,只需g(x)=0有且只有一个解,即方程e
x-bx=0有且只有一个解.
因为x=0不满足方程,所以方程同解于b=
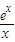
. …(6分)
令h(x)=
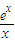
,由h′(x)=
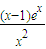
=0得x=1.
当x∈(1,+∞)时,h′(x)>0,h(x)单调递增,h(x)∈(e,+∞);
当x∈(0,1)时,h′(x)<0,h(x)单调递减,h(x)∈(e,+∞);
所以当x∈(0,+∞)时,方程b=
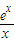
有且只有一解等价于b=e.…(8分)
当x∈(-∞,0)时,h(x)单调递减,且h(x)∈(-∞,0),
从而方程b=
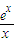
有且只有一解等价于b∈(-∞,0).
综上所述,b的取值范围为(-∞,0)∪{e}. …(10分)
(3)由g′(x)=e
x-b=0,得x=lnb.
当x∈(-∞,lnb)时,g′(x)<0,g(x)单调递减.
当x∈(lnb,+∞)时,g′(x)>0,g(x)单调递增.
所以在x=lnb时,g(x)取极小值g(lnb)=b-blnb=b(1-lnb).
①当0<b≤e时,g(lnb)=b-blnb=b(1-lnb)≥0,从而当x∈R时,g(x)≥0.
所以f(x)=|g(x)|=g(x)在(-∞,+∞)上无极大值.
因此,在x∈(0,2)上也无极大值. …(12分)
②当b>e时,g(lnb)<0.
因为g(0)=1>0,g(2lnb)=b
2-2blnb=b(b-2lnb)>0,
(令k(x)=x-2lnx.由k′(x)=1-
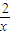
=0得x=2,从而当x∈(2,+∞)时,k(x)单调递增,
又k(e)=e-2>0,所以当b>e时,b-2lnb>0.)
所以存在x
1∈(0,lnb),x
2∈(lnb,2lnb),使得g(x
1)=g(x
2)=0.
此时f(x)=|g(x)|=
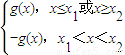
所以f(x)在(-∞,x
1)单调递减,在(x
1,lnb)上单调递增,在(lnb,x
2)单调递减,在(x
2,+∞)上单调递增. …(14分)
所以在x=lnb时,f(x)有极大值.
因为x∈(0,2),所以当lnb<2,即e<b<e
2时,f(x)在(0,2)上有极大值;
当lnb≥2,即b≥e
2 时,f(x)在(0,2)上不存在极大值.
综上所述,在区间(0,2)上,当0<b≤e或b≥e
2时,函数y=f(x)不存在极大值;
当e<b<e
2时,函数y=f(x),在x=lnb时取极大值f(lnb)=b(lnb-1).…(16分)
点评:本题考查导数知识的运用,考查函数的单调性,考查导数的几何意义,考查函数的极值,考查分类讨论的数学思想,难度较大.

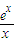 ,分类讨论可得当x∈(0,+∞)时,方程有且只有一解等价于b=e;当x∈(-∞,0)时,方程有且只有一解等价于b∈(-∞,0),从而可得b的取值范围;
,分类讨论可得当x∈(0,+∞)时,方程有且只有一解等价于b=e;当x∈(-∞,0)时,方程有且只有一解等价于b∈(-∞,0),从而可得b的取值范围;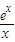 . …(6分)
. …(6分)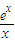 ,由h′(x)=
,由h′(x)=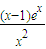 =0得x=1.
=0得x=1.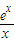 有且只有一解等价于b=e.…(8分)
有且只有一解等价于b=e.…(8分)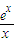 有且只有一解等价于b∈(-∞,0).
有且只有一解等价于b∈(-∞,0).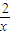 =0得x=2,从而当x∈(2,+∞)时,k(x)单调递增,
=0得x=2,从而当x∈(2,+∞)时,k(x)单调递增,