练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    已知三点P(4，
    		15
    )    、F1（3，0）、F2（-3，0）．求以F1、F2为焦点且过点P的双曲线的标准方程．
    分析：先根据双曲线上的点和焦点坐标，分别求得点到两焦点的距离二者相减求得a，进而根据焦点坐标求得c，进而求得b，则双曲线方程可得．
    解答：解：双曲线的焦点为（±3，0），c=3，|PF1|=
    		(4-3)2+(
    		15
    )    2
    =4    |PF2|=
    		(4+3)2+(
    		15
    )    2
    =8
    ∴2a=|PF2|-|PF1|=4
    得a=2，b=
    		32-22
    =
    		5
    ∴双曲线方程为
    x2
    4
    -
    y2
    5
    =1    ．
    点评：题主要考查了双曲线的标准方程．考查了学生对双曲线基础知识的理解和灵活把握．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    给出以下三个命题，其中所有正确命题的序号为
    ①
    ①

    ①已知等差数列{an}的前n项和为Sn，
    AO
    ，
    OB
    为不共线向量，又
    OP
    =a1
    OA
    +a2012
    OB
    ，若
    PA
    =λ
    PB
    ，则S2012=1006．
    ②“a=
    ∫
    1
    0
    		1-x2
    dx    ”是函数“y=cos2（ax）-sin2（ax）的最小正周期为4”的充要条件；
    ③已知函数f（x）=|x2-2|，若f（a）=f（b），且0＜a＜b，则动点P（a，b）到直线4x+3y-15=0的距离的最小值为1．

    查看答案和解析>>

    科目：高中数学 来源：2013届湖北省黄冈市高三上学期期末考试理科数学试卷（带解析） 题型：填空题

    给出以下三个命题，其中所有正确命题的序号为＿＿＿＿．
    ①已知等差数列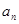｛｝的前二项和为，为不共线向量，又，
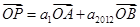    若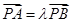，则S2012＝1006．
    ②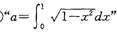是函数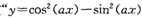的最小正周期为4"的充要条件；
    ③已知函数f (x)＝｜x2－2｜，若f (a) =" f" (b)，且0<a<b,则动点P(a,b)到直线4x＋3y－15=0的距离的最小值为1；

    查看答案和解析>>

    科目：高中数学 来源：2012-2013学年湖北省黄冈市高三上学期期末考试理科数学试卷（解析版） 题型：填空题

    给出以下三个命题，其中所有正确命题的序号为＿＿＿＿．

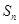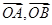    ①已知等差数列｛｝的前二项和为，为不共线向量，又，

    若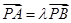，则S2012＝1006．

    ②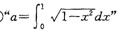是函数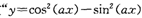的最小正周期为4"的充要条件；

    ③已知函数f (x)＝｜x2－2｜，若f (a) =" f" (b)，且0<a<b,则动点P(a,b)到直线4x＋3y－15=0的距离的最小值为1；

     

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    已知三点P(4，
    		15
    )    、F1（3，0）、F2（-3，0）．求以F1、F2为焦点且过点P的双曲线的标准方程．

    查看答案和解析>>

    同步练习册答案