
【题目】已知![]() 为奇函数,
为奇函数,![]() 为偶函数,且
为偶函数,且![]() .
.
(1)求函数![]() 及
及![]() 的解析式,并用函数单调性的定义证明:函数
的解析式,并用函数单调性的定义证明:函数![]() 在
在![]() 上是减函数;
上是减函数;
(2)若关于![]() 的方程
的方程![]() 有解,求实数
有解,求实数![]() 的取值范围.
的取值范围.
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 过点
过点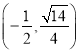 ,且离心率为
,且离心率为![]() .过点
.过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
, ![]() 两点.
两点.
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)若点![]() 为椭圆
为椭圆![]() 的右顶点,探究:
的右顶点,探究: ![]() 是否为定值,若是,求出该定值,若不是,请说明理由.(其中,
是否为定值,若是,求出该定值,若不是,请说明理由.(其中, ![]() ,
, ![]() 分别是直线
分别是直线![]() 、
、![]() 的斜率)
的斜率)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某电视台为宣传本省,随机对本省内![]() 岁的人群抽取了n人,回答问题“本省内著名旅游景点有哪些”统计结果如图表所示
岁的人群抽取了n人,回答问题“本省内著名旅游景点有哪些”统计结果如图表所示
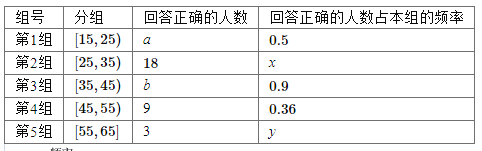
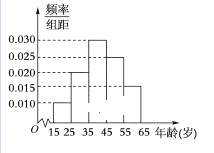
(1)分别求出![]() 的值;
的值;
(2)从第![]() 组回答正确的人中用分层抽样的方法抽取6人,求第
组回答正确的人中用分层抽样的方法抽取6人,求第![]() 组每组各抽取多少人?
组每组各抽取多少人?
(3)指出直方图中,这组数据的中位数是多少(取整数值)?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】旅行社为某旅行团包飞机去旅游,其中旅行社的包机费为15000元.旅游团中的每人的飞机票按以下方式与旅行社结算:若旅游团的人数不超过35人时,飞机票每张收费800元;若旅游团的人数多于35人,则给予优惠,每多1人,机票费每张减少10元,但旅游团的人数最多有60人.设旅行团的人数为![]() 人,飞机票价格为
人,飞机票价格为![]() 元,旅行社的利润为
元,旅行社的利润为![]() 元.
元.
(1)写出飞机票价格![]() 元与旅行团人数
元与旅行团人数![]() 之间的函数关系式;
之间的函数关系式;
(2)当旅游团的人数![]() 为多少时,旅行社可获得最大利润?求出最大利润.
为多少时,旅行社可获得最大利润?求出最大利润.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
在△ABC中,内角A,B,C所对的边分别为a,b,c.已知acosC+ccosA=2bcosA.
(1)求角A的值;
(2)求sinB+sinC的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(12分)已知函数f(x)=![]()
(1)判断函数在区间[1,+∞)上的单调性,并用定义证明你的结论.
(2)求该函数在区间[1,4]上的最大值与最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某桶装水经营部每天的房租、人员工资等固定成本为300元,每桶水的进价是8元,销售单价与日均销售量的关系如表所示:
销售单价/元 | 9 | 10 | 11 | 12 | 13 | 14 |
日均销售量/桶 | 550 | 500 | 450 | 400 | 350 | 300 |
请根据以上数据分析,这个店怎样定每桶水的单价才能获得最大利润?最大利润是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】袋子![]() 和
和![]() 中均装有若干个大小相同的红球和白球,从
中均装有若干个大小相同的红球和白球,从![]() 中摸出一个红球的概率是
中摸出一个红球的概率是![]() ,从
,从![]() 中摸出一个红球的概率为
中摸出一个红球的概率为![]() .
.
(1)从![]() 中有放回地摸球,每次摸出1个,有3次摸到红球即停止,求恰好摸5次停止的概率.
中有放回地摸球,每次摸出1个,有3次摸到红球即停止,求恰好摸5次停止的概率.
(2)若![]() 、
、![]() 两个袋子中的球数之比为
两个袋子中的球数之比为![]() ,将
,将![]() 、
、![]() 中的球装在一起后,从中摸出一个红球的概率是
中的球装在一起后,从中摸出一个红球的概率是![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com