
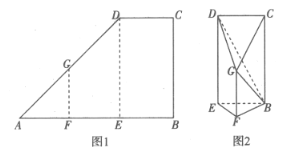
【题目】如图1,在直角梯形![]() 中,E,F分别为
中,E,F分别为![]() 的三等分点,
的三等分点,![]() ,
,![]() ,
,![]() ,
,![]() ,若沿着
,若沿着![]() ,
,![]() 折叠使得点A和点B重合,如图2所示,连结
折叠使得点A和点B重合,如图2所示,连结![]() ,
,![]() .
.
(1)求证:平面![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
【答案】(1)见解析(2)![]()
【解析】
(1)取![]() 的中点分别为
的中点分别为![]() ,连结
,连结![]() ,由已知
,由已知![]() 为等边三角形,可得
为等边三角形,可得![]() ,
,![]() 平面
平面![]() ,有
,有![]() ,进而证明
,进而证明![]() 平面
平面![]() ,再证明四边形
,再证明四边形![]() 为平行四边形,得到
为平行四边形,得到![]() ,所以有
,所以有![]() 平面
平面![]() 即可;
即可;
(2)以![]() 为坐标原点,建立如下图坐标系,求出
为坐标原点,建立如下图坐标系,求出![]() 坐标,分别求出平面
坐标,分别求出平面![]() 和
和
平面![]() 的法向量,按空间向量二面角公式,即可求解.
的法向量,按空间向量二面角公式,即可求解.
(1)取![]() ,
,![]() 的中点分别为O,M,连结
的中点分别为O,M,连结![]() ,
,![]() ,
,![]() .
.
![]() 且
且![]() ,又因为
,又因为![]() 且
且![]() ,
,
所以![]() 且
且![]() ,
,
故四边形![]() 为平行四边形,故
为平行四边形,故![]() .
.
因为M为![]() 中点,三角形
中点,三角形![]() 为等边三角形,故
为等边三角形,故![]() ,
,
因为![]() 平面
平面![]() 平面
平面![]() ,所以
,所以![]() ,
,
因为![]() ,所以
,所以![]() 平面
平面![]() ,
,
因此![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
故平面![]() 平面
平面![]() ;
;
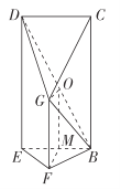
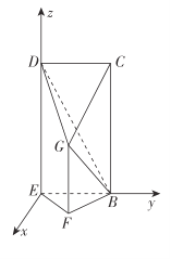
(2)建立如图所示的空间直角坐标系,
则![]() ,
,![]() ,
,![]() ,
,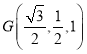 ,
,
则![]() ,
,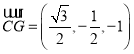 ,
,![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,则
,则
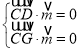 ,即
,即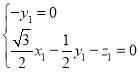 ,
,
令![]() 得
得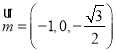 ;
;
设平面![]() 的法向量为
的法向量为![]() ,
,
则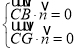 ,
,
即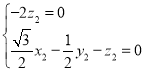 ,
,
令![]() ,得
,得![]() .
.
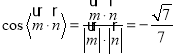 .
.
故二面角![]() 的余弦值为
的余弦值为![]() .
.


 步步高达标卷系列答案
步步高达标卷系列答案科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,曲线C的参数方程为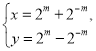 (m为参数),以O为极点,x轴的正半轴为极轴建立极坐标系,直线l的极坐标方程为
(m为参数),以O为极点,x轴的正半轴为极轴建立极坐标系,直线l的极坐标方程为![]() ρcosθ
ρcosθ![]() ρsinθ
ρsinθ![]() 2
2![]() =0.
=0.
(1)求C和l的直角坐标方程;
(2)设直线l与曲线C的公共点为P,Q,求|PQ|.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正三棱柱![]() 的所有棱长都为
的所有棱长都为![]() ,
,![]() 是
是![]() 的中点,
的中点,![]() 在
在![]() 边上,
边上,![]() .
.
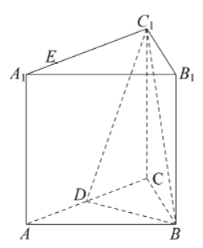
(1)证明:平面![]() 平面
平面![]() ;
;
(2)若![]() 是侧面
是侧面![]() 内的动点,且
内的动点,且![]() 平面
平面![]() .
.
①在答题卡中作出点![]() 的轨迹,并说明轨迹的形状(不需要说明理由);
的轨迹,并说明轨迹的形状(不需要说明理由);
②求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场一年中各月份的收入、支出情况的统计如图所示,下列说法中正确的是______.
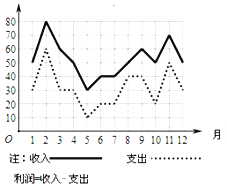
①2至3月份的收入的变化率与11至12月份的收入的变化率相同;
②支出最高值与支出最低值的比是6:1;
③第三季度平均收入为50万元;
④利润最高的月份是2月份。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() .把
.把![]() 沿着
沿着![]() 翻折至
翻折至![]() 的位置,
的位置,![]() 平面
平面![]() ,连结
,连结![]() ,如图2.
,如图2.
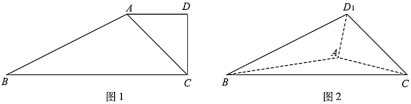
(1)当![]() 时,证明:平面
时,证明:平面![]() 平面
平面![]() ;
;
(2)当三棱锥![]() 的体积最大时,求点
的体积最大时,求点![]() 到平面
到平面![]() 的距离.
的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】渭南市公安局交警支队依据《中华人民共和国道路交通安全法》第![]() 条规定:渭南城区所有主干道路凡机动车途经十字口或斑马线,无论转弯或者直行,遇有行人过马路,必须礼让行人.违反者将被处以
条规定:渭南城区所有主干道路凡机动车途经十字口或斑马线,无论转弯或者直行,遇有行人过马路,必须礼让行人.违反者将被处以![]() 元罚款,记
元罚款,记![]() 分的行政处罚.下表是渭南市一主干路段,监控设备所抓拍的
分的行政处罚.下表是渭南市一主干路段,监控设备所抓拍的![]() 个月内,机动车驾驶员不“礼让斑马线”行为统计数据:
个月内,机动车驾驶员不“礼让斑马线”行为统计数据:
月份 |
|
|
|
|
|
违章驾驶员人数 |
|
|
|
|
|
(1)请利用所给数据求违章人数![]() 与月份
与月份![]() 之间的回归直线方程
之间的回归直线方程![]() ;
;
(2)预测该路![]() 月份的不“礼让斑马线”违章驾驶员人数;
月份的不“礼让斑马线”违章驾驶员人数;
(3)若从表中![]() 、
、![]() 月份分别抽取
月份分别抽取![]() 人和
人和![]() 人,然后再从中任选
人,然后再从中任选![]() 人进行交规调查,求拍到的两人恰好来自同一月份的概率.
人进行交规调查,求拍到的两人恰好来自同一月份的概率.
参考公式: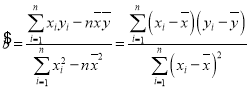 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知项数为![]() 的数列
的数列![]() 满足如下条件:①
满足如下条件:①![]() ;②
;②![]() .若数列
.若数列![]() 满足
满足![]() ,其中
,其中![]() 则称
则称![]() 为
为![]() 的“心灵契合数列”.
的“心灵契合数列”.
(I)数列1,5,9,11,15是否存在“心灵契合数列”若存在,写出其心灵契合数列,若不存在请说明理由;
(II)若![]() 为
为![]() 的“心灵契合数列”,判断数列
的“心灵契合数列”,判断数列![]() 的单调性,并予以证明;
的单调性,并予以证明;
(Ⅲ)已知数列![]() 存在“心灵契合数列”
存在“心灵契合数列”![]() ,且
,且![]() ,
,![]() ,求m的最大值.
,求m的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com