
【题目】设{an}是各项都为整数的等差数列,其前n项和为![]() ,
,![]() 是等比数列,且
是等比数列,且![]() ,
,![]() ,
,![]() ,
,![]() .
.
(1)求数列![]() ,
,![]() 的通项公式;
的通项公式;
(2)设cn=log2b1+log2b2+log2b3+…+log2bn, ![]() .
.
(i)求Tn;
(ii)求证: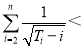 2.
2.
【答案】(1)![]() ,
,![]() ,
,![]() (2)(i)n3(ii)证明见解析;
(2)(i)n3(ii)证明见解析;
【解析】
(1)设等差数列{an}的公差为d,等比数列{bn}的公比为q,运用等差数列和等比数列的通项公式,解方程可得公差和公比,即可得到所求通项公式;
(2)(i)运用对数的运算性质和等差数列的求和公式可得![]() ,a
,a![]() n2﹣n﹣1+2i,再由数列的分组求和,结合等差数列的求和公式,计算可得所求和;
n2﹣n﹣1+2i,再由数列的分组求和,结合等差数列的求和公式,计算可得所求和;
(ii)推得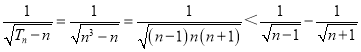 ,再由数列的裂项相消求和,结合不等式的性质,即可得证.
,再由数列的裂项相消求和,结合不等式的性质,即可得证.
解:(1)设等差数列{an}的公差为d,等比数列{bn}的公比为q,由![]() ,
,![]() ,
,![]() ,可得
,可得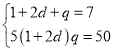 ,
,
解得d=2,q=2或d![]() ,q=5,
,q=5,
由于{an}是各项都为整数的等差数列,所以d=2,q=2,
从而![]() ,
,![]() ,
,![]() ;
;
(2)(i)∵log2bn=log22n﹣1=n﹣1,
∴cn=0+1+2+…+(n﹣1)![]() n(n﹣1),
n(n﹣1),
∴a![]() 2(
2(![]() i)﹣1=n2﹣n﹣1+2i,
i)﹣1=n2﹣n﹣1+2i,
∴Tn=(n2﹣n﹣1+2)+(n2﹣n﹣1+4)+…+(n2﹣n﹣1+2n)
=n(n2﹣n﹣1)+(2+4+…+2n)=n(n2﹣n﹣1)+n(n+1)=n3;
(ii)证明: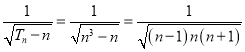
![]()
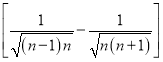
![]()
![]() ,
,
而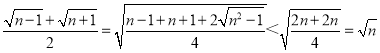 ,
,
∴![]() ,
,
∴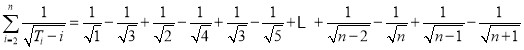
=1![]() ,
,
由于![]() 0,
0,
可得1![]() 2.
2.
则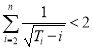 .
.


科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点为F,过F的直线交抛物线C于
的焦点为F,过F的直线交抛物线C于![]() ,
,![]() 两点.
两点.
(Ⅰ)当![]() 时,求
时,求![]() 的值;
的值;
(Ⅱ)过点A作抛物线准线的垂线,垂足为E,过点B作EF的垂线,交抛物线于另一点D,求![]() 面积的最小值.
面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知椭圆![]() 经过
经过![]() ,且右焦点坐标为
,且右焦点坐标为![]() .
.
(1)求椭圆的标准方程;
(2)设A,B为椭圆的左,右顶点,C为椭圆的上顶点,P为椭圆上任意一点(异于A,B两点),直线AC与直线BP相交于点M,直线BC与直线AP相交于点N,求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是椭圆
是椭圆![]() :
:![]() 上一点,以点
上一点,以点![]() 及椭圆的左、右焦点
及椭圆的左、右焦点![]() ,
,![]() 为顶点的三角形面积为
为顶点的三角形面积为![]() .
.
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)过![]() 作斜率存在且互相垂直的直线
作斜率存在且互相垂直的直线![]() ,
,![]() ,
,![]() 是
是![]() 与
与![]() 两交点的中点,
两交点的中点,![]() 是
是![]() 与
与![]() 两交点的中点,求△
两交点的中点,求△![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学高一、高二、高三年级的学生人数之比依次为6:5:7,防疫站欲对该校学生进行身体健康调查,用分层抽样的方法从该校高中三个年级的学生中抽取容量为n的样本,样本中高三年级的学生有21人,则n等于( )
A.35B.45C.54D.63
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为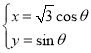 (
(![]() 为参数),在以原点O为极点,x的非负半轴为极轴建立的极坐标系中,直线
为参数),在以原点O为极点,x的非负半轴为极轴建立的极坐标系中,直线![]() 的极坐标方程为
的极坐标方程为![]()
(1)求曲线![]() 的普通方程和直线
的普通方程和直线![]() 的直角坐标方程;
的直角坐标方程;
(2)设直线![]() 与x轴,y轴分别交于A,B两点,点P是曲线
与x轴,y轴分别交于A,B两点,点P是曲线![]() 上任意一点,求
上任意一点,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】分形理论是当今世界十分风靡和活跃的新理论、新学科.其中把部分与整体以某种方式相似的形体称为分形.分形是一种具有自相似特性的现象.图象或者物理过程.标准的自相似分形是数学上的抽象,迭代生成无限精细的结构.也就是说,在分形中,每一组成部分都在特征上和整体相似,只仅仅是变小了一些而已.谢尔宾斯基三角形就是一种典型的分形,是由波兰数学家谢尔宾斯基在1915年提出的,其构造方法如下:取一个实心的等边三角形(如图1),沿三边的中点连线,将它分成四个小三角形,挖去中间的那一个小三角形(如图2),对其余三个小三角形重复上述过程(如图3).若图1(阴影部分)的面积为1,则图4(阴影部分)的面积为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a,b,c均为正数,设函数f(x)=|x﹣b|﹣|x+c|+a,x∈R.
(1)若a=2b=2c=2,求不等式f(x)<3的解集;
(2)若函数f(x)的最大值为1,证明:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题14分)在平面直角坐标系中,曲线C1的参数方程为![]() (a>b>0,
(a>b>0,![]() 为参数),以Ο为极点,x轴的正半轴为极轴建立极坐标系,曲线C2是圆心在极轴上且经过极点的圆,已知曲线C1上的点
为参数),以Ο为极点,x轴的正半轴为极轴建立极坐标系,曲线C2是圆心在极轴上且经过极点的圆,已知曲线C1上的点![]() 对应的参数
对应的参数![]() .
.![]() 与曲线C2交于点
与曲线C2交于点![]() .
.
(1)求曲线C1,C2的直角坐标方程;
(2)![]() ,
,![]() 是曲线C1上的两点,求
是曲线C1上的两点,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com