练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    集合M＝{－2，0，1}，N＝{1，2，3}，映射f：M→N，使任意x∈M，都有x＋f(x)＋xf(x)是奇数，则这样的映射只有

    [　　]

    A．10个

    B．12个

    C．13个

    D．15个

    答案：B
    解析：

    　　根据映射的定义求解，因为x∈M，只有3个值，可对其分类讨论．

    　　若x＝－2，－2＋f(－2)－2f(－2)＝－2(f(－2)＋1)＋f(－2)是奇数，f(－2)必为奇数，∴－2可以对应1或3；若x＝0，0＋f(0)＋0f(0)＝f(0)是奇数，f(0)必为奇数，

    　　∴0可以对应1或3；若x＝1，1＋f(1)＋f(1)＝2f(1)＋1是奇数，∴1可以对应1，2，3；∴满足条件的映射共为12个，故选B．


    提示：

    本题求映射个数问题．但有附加条件“x＋f(x)＋xf(x)是奇数”，故需分类求各种情况，然后用列举法．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知集合M＝{1，2，3，4}，，集合A中所有元素的乘积称为集合A的“累积值”，且规定：当集合A只有一个元素时，其累积值即为该元素的数值，空集的累积值为0. 设集合A的累积值为n.

    （1）若n＝3，则这样的集合A共有 2 个；（2）若n为偶数，则这样的集合A共有　　　个.

    查看答案和解析>>

    科目：高中数学 来源：2013届甘肃省高二下学期第二次月考文科数学试卷（解析版） 题型：选择题

    若集合M＝{x||x|≤2},N＝{x|x2-3x＝0},则M∩N等于                （    ）

    A.{3}             B.{0}             C.{0,2}             D.{0,3}

     

    查看答案和解析>>

    科目：高中数学 来源：2010-2011学年江西省高三10月月考理科数学卷 题型：填空题

    已知集合M＝{1，2，3，4}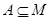，，集合A中所有元素的乘积称为集合A

    的“累积值”，且规定：当集合A只有一个元素时，其累积值即为该元素的数值，空集的累

    积值为0. 设集合A的累积值为n.，则使n为偶数的集合A共有          个.

     

    查看答案和解析>>

    科目：高中数学 来源：2012届湖北省高二下学期期末联考文科数学 题型：选择题

    若集合M＝{x||x|≤2},N＝{x|x2-3x＝0},则M∩N等于                （    ）

    A.{3}             B.{0}             C.{0,2}             D.{0,3}

     

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    设n、k为互素自然数，0＜k＜n，在集合M＝{1，2，…，n－1｝(n≥3)中的各数，要么着蓝色，要么着白色，已知

    (1)对于各i∈M，i和n－i同色；

    (2)对于各i∈M，i≠k， i和|i－k|同色．

    证明：在M中的所有数均同色．

    查看答案和解析>>

    同步练习册答案