
在 中,
中,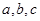 分别是角
分别是角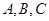 的对边,且
的对边,且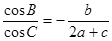 .
.
(1)求角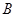 的大小;
的大小;
(2)若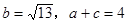 ,求
,求 的面积.
的面积.
科目:高中数学 来源: 题型:解答题
已知甲船正在大海上航行,当它位于A处时获悉,在其正东方向相距20海里的B处有一艘渔船遇险等待营救,甲船立即以10海里/小时的速度匀速前往救援,同时把消息告知在甲船的南偏西 ,相距10海里C处的乙船,乙船当即决定匀速前往救援,并且与甲船同时到达。(供参考使用:
,相距10海里C处的乙船,乙船当即决定匀速前往救援,并且与甲船同时到达。(供参考使用: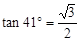 ).
).
(1)试问乙船航行速度的大小;
(2)试问乙船航行的方向(试用方位角表示,如北偏东…度).
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
在△ABC中,A、B、C所对的边分别是a、b、c,且bcosB是acosC、ccosA的等差中项.
(1)求B的大小;
(2)若a+c= ,b=2,求△ABC的面积.
,b=2,求△ABC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com