
【题目】“中国人均读书4.3本(包括网络文学和教科书),比韩国的11本、法国的20本、日本的40本、犹太人的64本少得多,是世界上人均读书最少的国家.”这个论断被各种媒体反复引用,出现这样的统计结果无疑是令人尴尬的,而且和其他国家相比,我国国民的阅读量如此之低,也和我国是传统的文明古国、礼仪之邦的地位不相符.某小区为了提高小区内人员的读书兴趣,特举办读书活动,准备进一定量的书籍丰富小区图书站,由于不同年龄段需看不同类型的书籍,为了合理配备资源,现对小区内看书人员进行年龄调查,随机抽取了一天40名读书者进行调查,将他们的年龄分成6段: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 后得到如图所示的频率分布直方图.问:
后得到如图所示的频率分布直方图.问:
(1)估计在40名读书者中年龄分布在![]() 的人数;
的人数;
(2)求40名读书者年龄的平均数和中位数;
(3)若从年龄在![]() 的读书者中任取2名,求这两名读书者年龄在
的读书者中任取2名,求这两名读书者年龄在![]() 的人数
的人数![]() 的分布列及数学期望.
的分布列及数学期望.

【答案】(1)30;(2)54,55;(3) ![]() 的分布列如下:
的分布列如下:
| 0 | 1 | 2 |
|
|
|
|
数学期望![]()
【解析】试题分析:(1)由频率分布直方图知年龄在[40,70)的频率为(0.020+0.030+0.025)×10,进而得出40名读书者中年龄分布在[40,70)的人数.(2)40名读书者年龄的平均数为25×0.05+35×0.1+45×0.2+55×0.3+65×0.25+75×0.1.计算频率为![]() 处所对应的数据即可得出中位数.(3)年龄在[20,30)的读书者有2人,年龄在[30,40)的读书者有4人,所以X的所有可能取值是0,1,2.利用超几何分布列计算公式即可得出.
处所对应的数据即可得出中位数.(3)年龄在[20,30)的读书者有2人,年龄在[30,40)的读书者有4人,所以X的所有可能取值是0,1,2.利用超几何分布列计算公式即可得出.
试题解析:
(1)由频率分布直方图知年龄在![]() 的频率为
的频率为![]() ,
,
所以40名读书者中年龄分布在![]() 的人数为
的人数为![]() .
.
(2)40名读书者年龄的平均数为
![]()
![]() .
.
设中位数为![]() ,则
,则![]()
解得![]() ,即40名读书者年龄的中位数为55.
,即40名读书者年龄的中位数为55.
(3)年龄在![]() 的读书者有
的读书者有![]() 人,
人,
年龄在![]() 的读书者有
的读书者有![]() 人,
人,
所以![]() 的所有可能取值是0,1,2,
的所有可能取值是0,1,2,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 的分布列如下:
的分布列如下:
| 0 | 1 | 2 |
|
|
|
|
数学期望![]() .
.


科目:高中数学 来源: 题型:
【题目】(导学号:05856334)
已知函数f(x)=ln x+ax2+1.
(Ⅰ)当a=-1时,求函数f(x)的极值;
(Ⅱ)当a>0时,证明:存在正实数λ,使得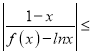 λ恒成立.
λ恒成立.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】据某气象中心观察和预测:发生于M地的沙尘暴一直向正南方向移动,其移动速度v(km/h)与时间t(h)的函数图象如图所示.过线段OC上一点T(t,0)作横轴的垂线l,梯形OABC在直线l左侧部分的面积即时间t(h)内沙尘暴所经过的路程s(km).
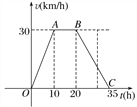
(1)当t=4时,求s的值;
(2)将s随t变化的规律用数学关系式表示出来;
(3)若N城位于M地正南方向,且距M地650 km,试判断这场沙尘暴是否会侵袭到N城,如果会,在沙尘暴发生后多长时间它将侵袭到N城?如果不会,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,椭圆![]() 的右顶点为
的右顶点为![]() ,左、右焦点分别为
,左、右焦点分别为![]() ,过点
,过点![]() 且斜率为
且斜率为![]() 的直线与
的直线与![]() 轴交于点
轴交于点![]() ,与椭圆交于另一个点
,与椭圆交于另一个点![]() ,且点
,且点![]() 在
在![]() 轴上的射影恰好为点
轴上的射影恰好为点![]() .
.

(1)求椭圆![]() 的标准方程;
的标准方程;
(2)过点![]() 的直线与椭圆交于
的直线与椭圆交于![]() 两点(
两点(![]() 不与
不与![]() 重合),若
重合),若![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)是定义在R上的奇函数,当x>0时, ![]() .给出以下命题:
.给出以下命题:
①当x<0时,f(x)=ex(x+1);
②函数f(x)有五个零点;
③若关于x的方程f(x)=m有解,则实数m的取值范围是f(-2)≤m≤f(2);
④对x1,x2∈R,|f(x2)-f(x1)|<2恒成立.
其中,正确命题的序号是________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com