
对于下列命题:①若 ,则角
,则角 的终边在第三、四象限;②若点
的终边在第三、四象限;②若点 在函数
在函数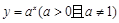 的图象上,则点
的图象上,则点 必在函数
必在函数 的图象上;③若角
的图象上;③若角 与角
与角 的终边成一条直线,则
的终边成一条直线,则 ;④幂函数的图象必过点(1,1)与(0,0).其中所有正确命题的序号是
;④幂函数的图象必过点(1,1)与(0,0).其中所有正确命题的序号是
A.①③ B.② C.③④ D.②④
B
【解析】
试题分析:判定各个命题的正确性,然后确定结论。
命题1中,由于 ,则说明角
,则说明角 的终边在y轴的下方,可能在y轴的负半轴上,因此错误。
的终边在y轴的下方,可能在y轴的负半轴上,因此错误。
命题2中,点P(2,4)在指数函数图像上,说明可知4=a ,a>0,故可知a=2,那么对数函数
,a>0,故可知a=2,那么对数函数 ,显然可知点(4,2)点代入满足等式,故成立。
,显然可知点(4,2)点代入满足等式,故成立。
命题3中,角 与角
与角 的终边成一条直线且为y轴时,正切值不存在,因此错误。
的终边成一条直线且为y轴时,正切值不存在,因此错误。
命题4中,幂函数 过点(1,1),(0,0),当
过点(1,1),(0,0),当 是负数的时候不成立。不过点(0,0)
是负数的时候不成立。不过点(0,0)
故选B。
考点:本试题主要是考查了基本初等函数的性质运用
点评:解决该试题的关键就是要理解函数图像与点的位置关系的判定,以及三角函数中正切值存在的前提条件,,熟悉三角函数的符号,以及幂函数的解析式,属于中档题。


 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案科目:高中数学 来源: 题型:
|
| 1 |
| 2 |
| x1+x2 |
| 2 |
| f(x1)+f(x2) |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| π |
| 6 |
| 2012π |
| 3 |
| 2012π |
| 3 |
| 2012π |
| 3 |
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| π |
| 6 |
| 2012π |
| 3 |
| 2012π |
| 3 |
| 2012π |
| 3 |
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| f(x1)+f(x2) |
| 2 |
| x1+x2 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com