
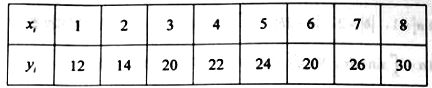
【题目】某房产中介公司2017年9月1日正式开业,现对其每个月的二手房成交量进行统计,![]() 表示开业第
表示开业第![]() 个月的二手房成交量,得到统计表格如下:
个月的二手房成交量,得到统计表格如下:
(1)统计中常用相关系数![]() 来衡量两个变量之间线性关系的强弱.统计学认为,对于变量
来衡量两个变量之间线性关系的强弱.统计学认为,对于变量![]() ,如果
,如果![]() ,那么相关性很强;如果
,那么相关性很强;如果![]() ,那么相关性一般;如果
,那么相关性一般;如果![]() ,那么相关性较弱.通过散点图初步分析可用线性回归模型拟合
,那么相关性较弱.通过散点图初步分析可用线性回归模型拟合![]() 与
与![]() 的关系.计算
的关系.计算![]() 的相关系数
的相关系数![]() ,并回答是否可以认为两个变量具有很强的线性相关关系(计算结果精确到0.01)
,并回答是否可以认为两个变量具有很强的线性相关关系(计算结果精确到0.01)
(2)请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() (计算结果精确到0.01),并预测该房产中介公司2018年6月份的二手房成交量(计算结果四舍五入取整数).
(计算结果精确到0.01),并预测该房产中介公司2018年6月份的二手房成交量(计算结果四舍五入取整数).
(3)该房产中介为增加业绩,决定针对二手房成交客户开展抽奖活动.若抽中“一等奖”获6千元奖金;抽中“二等奖”获3千元奖金;抽中“祝您平安”,则没有奖金.已知一次抽奖活动中获得“一等奖”的概率为![]() ,获得“二等奖”的概率为
,获得“二等奖”的概率为![]() ,现有甲、乙两个客户参与抽奖活动,假设他们是否中奖相互独立,求此二人所获奖金总额
,现有甲、乙两个客户参与抽奖活动,假设他们是否中奖相互独立,求此二人所获奖金总额![]() (千元)的分布列及数学期望.
(千元)的分布列及数学期望.
参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
参考公式: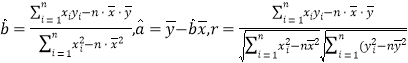
科目:高中数学 来源: 题型:
【题目】某小组为了研究昼夜温差对一种稻谷种子发芽情况的影响,他们分别记录了4月1日至4月5日的每天星夜温差与实验室每天每100颗种子的发芽数,得到如下资料:
日期 | 4月1日 | 4月2日 | 4月3日 | 4月4日 | 4月5日 |
温差 | 9 | 10 | 11 | 8 | 12 |
发芽数 | 38 | 30 | 24 | 41 | 17 |
利用散点图,可知![]() 线性相关。
线性相关。
(1)求出![]() 关于
关于![]() 的线性回归方程,若4月6日星夜温差
的线性回归方程,若4月6日星夜温差![]() ,请根据你求得的线性同归方程预测4月6日这一天实验室每100颗种子中发芽颗数;
,请根据你求得的线性同归方程预测4月6日这一天实验室每100颗种子中发芽颗数;
(2)若从4月1日![]() 4月5日的五组实验数据中选取2组数据,求这两组恰好是不相邻两天数据的概率.
4月5日的五组实验数据中选取2组数据,求这两组恰好是不相邻两天数据的概率.
(公式: )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下面几个命题中,假命题是( )
A. “若![]() ,则
,则![]() ”的否命题
”的否命题
B. “![]() ,函数
,函数![]() 在定义域内单调递增”的否定
在定义域内单调递增”的否定
C. “![]() 是函数
是函数![]() 的一个周期”或“
的一个周期”或“![]() 是函数
是函数![]() 的一个周期”
的一个周期”
D. “![]() ”是“
”是“![]() ”的必要条件
”的必要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将圆![]() 上每一点的横坐标保持不变,纵坐标变为原来的
上每一点的横坐标保持不变,纵坐标变为原来的![]() 倍,得曲线
倍,得曲线![]() .
.
![]() 写出
写出![]() 的参数方程;
的参数方程;
![]() 设直线
设直线![]() 与
与![]() 的交点为
的交点为![]() ,以坐标原点为极点,
,以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系,求过线段
轴正半轴为极轴建立极坐标系,求过线段![]() 的中点且与
的中点且与![]() 垂直的直线的极坐标方程.
垂直的直线的极坐标方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若一条直线与一个平面垂直,则称此直线与平面构成一个“正交线面对”.那么在一个正方体中,由两个顶点确定的直线与含有四个顶点的平面构成的“正交线面对”的个数是( )
A. 48 B. 36 C. 24 D. 18
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】通过随机询问110名性别不同的大学生是否爱好体育,得到表:

参照附表,得到的正确结论是![]()
![]()
附:由公式算得:![]()
附表:
| 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| 1.323 | 2.702 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
A. 有![]() 以上的把握认为“爱好体育运动与性别有关”
以上的把握认为“爱好体育运动与性别有关”
B. 有![]() 以上的把握认为“爱好体育运动与性别无关”
以上的把握认为“爱好体育运动与性别无关”
C. 在犯错误的概率不超过![]() 的前提下,认为“爱好体育运动与性别有关”
的前提下,认为“爱好体育运动与性别有关”
D. 在犯错误的概率不超过![]() 的前提下,认为“爱好体育运动与性别无关”
的前提下,认为“爱好体育运动与性别无关”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,直四棱柱ABCD–A1B1C1D1的底面是菱形,AA1=4,AB=2,∠BAD=60°,E,M,N分别是BC,BB1,A1D的中点.

(1)证明:MN∥平面C1DE;
(2)求AM与平面A1MD所成角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com