
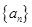 ,若
,若 ,且
,且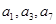 成等比数列,则此样本的平均数和中位数分别是( )
成等比数列,则此样本的平均数和中位数分别是( )A.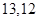 | B.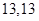 | C.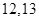 | D.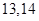 |
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案科目:高中数学 来源:不详 题型:解答题


查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.7,5,8 | B.9,5,6 | C.6,5,9 | D.8,5,7 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| | 硕士 | 博士 | 合计 |
| 男 | 162 | 27 | 189 |
| 女 | 143 | 8 | 151 |
| 合计 | 305 | 35 | 340 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
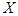 表示一位申请者经过考试的次数,据统计数据分析知
表示一位申请者经过考试的次数,据统计数据分析知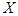 的概率分布如下:
的概率分布如下: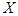 | 1 | 2 | 3 | 4 |
| P | 0.1 | 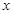 | 0.3 | 0.1 |
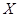 次考试需缴纳费用
次考试需缴纳费用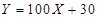 (单位:元),求两位申请者所需费用的和小于500元的概率;
(单位:元),求两位申请者所需费用的和小于500元的概率;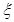 ,求
,求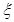 的分布列.
的分布列.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.10 | B.9 | C.8 | D.7 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 如下,其中拟合效果最好的模型是________.
如下,其中拟合效果最好的模型是________. 为-0.98;②模型Ⅱ的相关系数
为-0.98;②模型Ⅱ的相关系数 为0.80;
为0.80; 为-0.50;④模型Ⅳ的相关系数
为-0.50;④模型Ⅳ的相关系数 为0.25.
为0.25.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com