(本题满分15分)
已知各项均为正数的数列
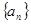
中,数列的前
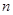
项和
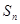
满足
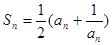
.
(1)求
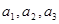
;
(2)由(1)猜想数列
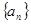
的通项公式,并用数学归纳法证明你的猜想.
(1)
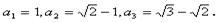
(2)见解析
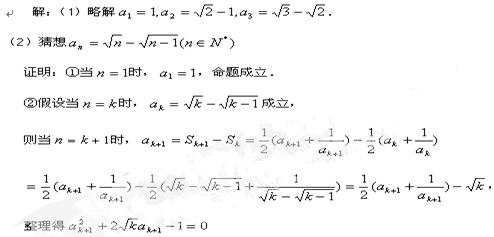
解得
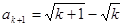
或
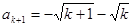
(舍),
即当
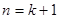
时,命题也成立.
由①②可知,对任意
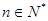
,
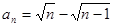
都成立.
练习册系列答案
相关习题
科目:高中数学
来源:不详
题型:解答题
(12分)已知数列

是等比数列,首项

(Ⅰ)求数列

的通项公式(Ⅱ)若数列

是等差数列,且

,求数列

的通项公式及前

项的和
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
等比数列
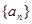
中,
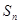
是前
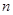
项和,若
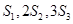
成等差数列,则数列
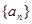
的公比为
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
设数列
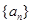
的前
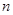
项和为
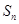
,
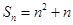
,数列
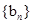
的通项公式为
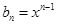
.
(1)求数列
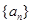
的通项公式;
(2)设
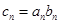
,数列
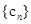
的前
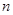
项和为
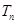
,
①求
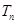
;
②若
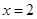
,求数列

的最小项的值.
查看答案和解析>>
科目:高中数学
来源:不详
题型:填空题
若

为


的各位数字之和,如

,

,则

;记

,

,…,

,

,则

=
.
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
等差数列{a
n}中,a
1+a
5=10,a
4=7,则数列{a
n}的公差为
查看答案和解析>>

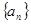 中,数列的前
中,数列的前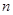 项和
项和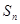 满足
满足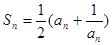 .
.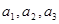 ;
;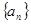 的通项公式,并用数学归纳法证明你的猜想.
的通项公式,并用数学归纳法证明你的猜想.