
����Ŀ���ҹ�������������ȱˮ�Ĺ��ң�����ȱˮ�����Ϊͻ����ij������Ϊ�˹��������Լ��ˮ���ƻ��ڱ������о���������ˮ�����������ȷ��һ�������ľ�������ˮ����������λ���֣�����ˮ��������![]() �IJ��ְ�ƽ���շѣ�����
�IJ��ְ�ƽ���շѣ�����![]() �IJ��ְ�����շѣ�Ϊ���˽�ȫ����������ˮ���ֲ������ͨ�������������100λ����ij�������ˮ������λ���֣��������ݰ���
�IJ��ְ�����շѣ�Ϊ���˽�ȫ����������ˮ���ֲ������ͨ�������������100λ����ij�������ˮ������λ���֣��������ݰ���![]() ����
����![]() �ֳ�9�飬�Ƴ�����ͼ��ʾ��Ƶ�ʷֲ�ֱ��ͼ
�ֳ�9�飬�Ƴ�����ͼ��ʾ��Ƶ�ʷֲ�ֱ��ͼ

��1����Ƶ�ʷֲ�ֱ��ͼ��![]() ��ֵ��
��ֵ��
��2����������������ʹ85%�ľ���ÿ�µ���ˮ����������![]() ���֣�������
���֣�������![]() ��ֵ����˵�����ɡ�
��ֵ����˵�����ɡ�
���𰸡���1��0.30����2����������ˮ����Ϊ2.9�֣�85%�ľ���ÿ�µ���ˮ����������
��������
��1������Ƶ�ʷ�ֱ��ͼ�еľ�������ĺ�Ϊ1��![]() ����
����
��2���ȴ������һ��![]() ���ڵ����䣬�ٸ�������
���ڵ����䣬�ٸ�������![]() ��Ƶ��֮��Ϊ0.85�����
��Ƶ��֮��Ϊ0.85�����![]() ��ֵ
��ֵ
��1����ֱ��ͼ���ɵ�![]() ��
��
���![]() .
.
��2����Ϊǰ6��Ƶ��֮��Ϊ
![]()
��ǰ5���Ƶ��֮��Ϊ
![]()
����![]() .
.
��![]()
���![]() .��ˣ���������ˮ����Ϊ2.9�֣�85%�ľ���ÿ�µ���ˮ����������.
.��ˣ���������ˮ����Ϊ2.9�֣�85%�ľ���ÿ�µ���ˮ����������.


 ���ĺ����Ͼ�������ϵ�д�
���ĺ����Ͼ�������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������A��BCD���ⳤΪa����E��F�ֱ�����BD��BC���е㣬��ƽ��AEF�ظ�������������������ý�������Ϊ_____.
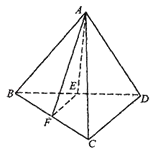
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ������
������![]() .
.
����a=1ʱ������![]() �ĵ������䣺
�ĵ������䣺
��������![]() �ļ�ֵ��
�ļ�ֵ��
����������![]() ��������ͬ����㣬��a��ȡֵ��Χ��
��������ͬ����㣬��a��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�����ڽ��д����������еĻ�У�Ϊ�˽����ԡ����ġ�������̶ȣ���֯��������֣�����Ϊ����������Ϊ100�֣������������ȡһ������Ϊ120�������������������ݾ���![]() �ڣ��ֽ���Щ�����ֳ�����6�鲢������������Ƶ�ʷֲ�ֱ��ͼ������С�������˲���ͼ�Σ���ͼ��ʾ���۲�ͼ�Σ��ش��������⣺
�ڣ��ֽ���Щ�����ֳ�����6�鲢������������Ƶ�ʷֲ�ֱ��ͼ������С�������˲���ͼ�Σ���ͼ��ʾ���۲�ͼ�Σ��ش��������⣺

��1�����������![]() ��Ƶ��������ȫƵ�ʷֲ�ֱ��ͼ��
��Ƶ��������ȫƵ�ʷֲ�ֱ��ͼ��
��2�������Ƶ�ʷֲ�ֱ��ͼ��������������������λ����ƽ��������ÿ��������������е�ֵΪ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڼ�����ϵ�£�����![]() ��ͼ��Ϊ��ͼ��ʾ�ġ�������Ҷ�ݡ����ֳ�Ϊõ���ߣ�
��ͼ��Ϊ��ͼ��ʾ�ġ�������Ҷ�ݡ����ֳ�Ϊõ���ߣ�
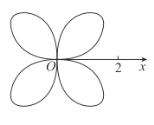
��1����õ���ߵ�![]() ʱ�����Լ���ΪԲ�ĵĵ�λԲ��õ���ߵĽ���ļ����ꣻ
ʱ�����Լ���ΪԲ�ĵĵ�λԲ��õ���ߵĽ���ļ����ꣻ
��2��������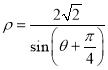 �ϵĵ�M��õ�����ϵĵ�N�������Сֵ��ȡ����Сֵʱ�ĵ�M��N�ļ����꣨����д��ϸ������̣���
�ϵĵ�M��õ�����ϵĵ�N�������Сֵ��ȡ����Сֵʱ�ĵ�M��N�ļ����꣨����д��ϸ������̣���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��5�Ž�ȯ����2�����н��ģ����ɼ׳�1�ţ�Ȼ�����ҳ�1�ţ���Żأ���:
��1�����н��ĸ���![]() ��
��
��2���ס��Ҷ��н��ĸ���![]() ��
��
��3��ֻ�����н��ĸ���![]() ��
��
��4�����н��ĸ���![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������Բ![]() (a>b>0)����ΪF���϶���ΪB. ��֪��Բ��������Ϊ
(a>b>0)����ΪF���϶���ΪB. ��֪��Բ��������Ϊ![]() ����A������Ϊ
����A������Ϊ![]() ����
����![]() .
.
��I������Բ�ķ��̣�
��II����ֱ��l�� ![]() ����Բ�ڵ�һ���Ľ���ΪP����l��ֱ��AB���ڵ�Q. ��
����Բ�ڵ�һ���Ľ���ΪP����l��ֱ��AB���ڵ�Q. ��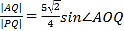 (OΪԭ��) ����k��ֵ.
(OΪԭ��) ����k��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������![]() ��ǰ
��ǰ![]() ���Ϊ
���Ϊ![]() ����
����![]() ������
������![]() Ϊ�Ȳ����У���
Ϊ�Ȳ����У���![]() ��
��![]() .
.
��1��������![]() ��
��![]() ��ͨ�ʽ��
��ͨ�ʽ��
��2����![]() ��������
��������![]() ��ǰ
��ǰ![]() ���
���![]() ��
��
��3����������������![]() ������ʽ
������ʽ![]() ����������
����������![]() �����ֵ.
�����ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() �IJ���ͼ����ͼ��ʾ.
�IJ���ͼ����ͼ��ʾ.

��1����![]() ��ֵ��
��ֵ��
��2����![]() ��
��![]() �ϵ����ֵ����Сֵ��
�ϵ����ֵ����Сֵ��
��3������ͼ��˵������![]() ��ͼ�����
��ͼ�����![]() ��ͼ�������仯�õ�.
��ͼ�������仯�õ�.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com