
【题目】设函数f(x)=|x|x+bx+c,给出下列4个命题:
①b=0,c>0时,方程f(x)=0只有一个实数根;
②c=0时,y=f(x)是奇函数;
③y=f(x)的图象关于点(0,c)对称;
④方程f(x)=0至多有2个不相等的实数根.
上述命题中的所有正确命题的序号是 .
【答案】①②③
【解析】解:①当b=0,c>0时,f(x)=|x|x+c= 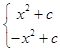 ,结合图形知f(x)=0只有一个实数根,故①正确;②当c=0时,f(x)=|x|x+bx,有f(﹣x)=﹣f(x)=﹣|x|x﹣bx,故y=f(x)是奇函数,故②正确;③y=f(x)的图象可由奇函数f(x)=|x|x+bx,向上或向下平移|c|而得到,y=f(x)的图象与y轴交点为(0,c),故函数y=f(x)的图象关于(0,c)对称,故③正确;④当b=﹣5,c=6时,方程|x|x﹣5x+6=0有三个解﹣6、2、3,即三个零点,故④错误;所以答案是:①②③.
,结合图形知f(x)=0只有一个实数根,故①正确;②当c=0时,f(x)=|x|x+bx,有f(﹣x)=﹣f(x)=﹣|x|x﹣bx,故y=f(x)是奇函数,故②正确;③y=f(x)的图象可由奇函数f(x)=|x|x+bx,向上或向下平移|c|而得到,y=f(x)的图象与y轴交点为(0,c),故函数y=f(x)的图象关于(0,c)对称,故③正确;④当b=﹣5,c=6时,方程|x|x﹣5x+6=0有三个解﹣6、2、3,即三个零点,故④错误;所以答案是:①②③.
【考点精析】掌握命题的真假判断与应用是解答本题的根本,需要知道两个命题互为逆否命题,它们有相同的真假性;两个命题为互逆命题或互否命题,它们的真假性没有关系.


科目:高中数学 来源: 题型:
【题目】已知圆心在y轴上的圆C经过点A(1,2)和点B(0,3).
(Ⅰ)求圆C的方程;
(Ⅱ)若直线l在两坐标轴上的截距相等,且被圆C截得的弦长为 ![]() ,求l的方程.
,求l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(文)已知y=f(x)是偶函数,y=g(x)是奇函数,它们的定义域均为[﹣3,3],且它们在x∈[0,3]上的图象如图所示,则不等式 ![]() 的解集是
的解集是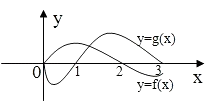
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知关于x的不等式x2﹣ax﹣2>0的解集为{x|x<﹣1或x>b}(b>﹣1).
(1)求a,b的值;
(2)当m>﹣ ![]() 时,解关于x的不等式(mx+a)(x﹣b)>0.
时,解关于x的不等式(mx+a)(x﹣b)>0.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为方便市民休闲观光,市政府计划在半径为200米,圆心角为120°的扇形广场内(如图所示),沿△ABC边界修建观光道路,其中A、B分别在线段CP、CQ上,且A、B两点间距离为定长 ![]() 米.
米. 
(1)当∠BAC=45°时,求观光道BC段的长度;
(2)为提高观光效果,应尽量增加观光道路总长度,试确定图中A、B两点的位置,使观光道路总长度达到最长?并求出总长度的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列四个命题:
①已知M={(x,y)| ![]() =3},N={(x,y)|ax+2y+a=0}且M∩N=,则a=﹣6;
=3},N={(x,y)|ax+2y+a=0}且M∩N=,则a=﹣6;
②已知点A(x1 , y1),B(x2 , y2),则以AB为直径的圆的方程是(x﹣x1)(x﹣x2)+(y﹣y1)(y﹣y2)=0;
③ ![]() =1(a≠b)表示焦点在x轴上的椭圆;
=1(a≠b)表示焦点在x轴上的椭圆;
④已知抛物线y2=2px(p>0)的焦点弦AB的两端点坐标分别为A(x1 , y2),B(x2 , y2),则 ![]() =﹣4
=﹣4
其中的真命题是 . (把你认为是真命题的序号都填上)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com