
【题目】如图,在四棱锥![]() 中,
中, ![]() ,
, ![]() 平面
平面![]() ,
, ![]() .
.
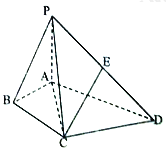
(1)设点![]() 为
为![]() 的中点,求证:
的中点,求证: ![]() 平面
平面![]() ;
;
(2)线段![]() 上是否存在一点
上是否存在一点![]() ,使得直线
,使得直线![]() 与平面
与平面![]() 所成的角
所成的角![]() 的正弦值为
的正弦值为![]() ?若存在,试确定点
?若存在,试确定点![]() 的位置;若不存在,请说明理由.
的位置;若不存在,请说明理由.
【答案】(1)见解析(2)![]() 为
为![]() 中点
中点
【解析】试题分析:(1)先取![]() 的中点
的中点![]() ,利用三角形中位线性质得
,利用三角形中位线性质得![]() ,再根据线面平行判定定理得
,再根据线面平行判定定理得![]() 平面
平面![]() .根据计算,利用平几知识得
.根据计算,利用平几知识得![]() ,再根据线面平行判定定理得
,再根据线面平行判定定理得![]() 平面
平面![]() .从而利用面面平行判定定理得平面
.从而利用面面平行判定定理得平面![]() 平面
平面![]() .最后根据面面平行性质得
.最后根据面面平行性质得![]() 平面
平面![]() . (2)一般利用空间直角坐标系研究线面角,先根据条件建立恰当直角坐标系,设立各点坐标,利用方程组求出平面法向量,根据向量数量积求出向量夹角,最后利用线面角与向量夹角关系列方程,解出点
. (2)一般利用空间直角坐标系研究线面角,先根据条件建立恰当直角坐标系,设立各点坐标,利用方程组求出平面法向量,根据向量数量积求出向量夹角,最后利用线面角与向量夹角关系列方程,解出点![]() 坐标,确定其位置.
坐标,确定其位置.
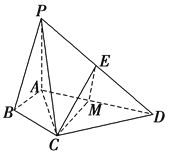
试题解析:(1)证明 取![]() 的中点
的中点![]() ,连接
,连接![]() ,则
,则![]() .
.
因为![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() .
.
在![]() 中,
中, ![]() ,所以
,所以![]() .
.
而![]() ,所以
,所以![]() .
.
因为![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
又因为![]() ,
,
所以平面![]() 平面
平面![]() .
.
因为![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
(注:(1)问也可建系来证明)
(2)过![]() 作
作![]() ,交
,交![]() 于
于![]() ,又
,又![]() 平面
平面![]() 知以
知以![]() 为原点,
为原点, ![]() 分别为
分别为![]() 轴建系如图:
轴建系如图:
则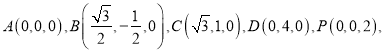
设平面PAC的法向量![]() ,
,
由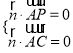 有
有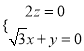 取
取![]()
设![]() ,则
,则![]() ,
,
∴![]()
∴
∴![]() ,∴
,∴![]() .
.
∴线段![]() 上存在一点
上存在一点![]() ,
, ![]() 为
为![]() 中点
中点


科目:高中数学 来源: 题型:
【题目】【山东省实验中学2017届高三第一次诊断】已知椭圆![]() :
:![]() 的右焦点
的右焦点![]() ,过点
,过点![]() 且与坐标轴不垂直的直线与椭圆交于
且与坐标轴不垂直的直线与椭圆交于![]() ,
,![]() 两点,当直线
两点,当直线![]() 经过椭圆的一个顶点时其倾斜角恰好为
经过椭圆的一个顶点时其倾斜角恰好为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设![]() 为坐标原点,线段
为坐标原点,线段![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() ?若存在,求出实数
?若存在,求出实数![]() 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△ABC的顶点A(5,1),AB边上的中线CM所在直线方程为2x﹣y﹣5=0,AC边上的高BH所在直线方程为x﹣2y﹣5=0.求:
(1)顶点C的坐标;
(2)直线BC的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() 的右焦点为
的右焦点为![]() ,离心率为
,离心率为![]() ,过点
,过点![]() 且与
且与![]() 轴垂直的直线被椭圆截得的线段长为
轴垂直的直线被椭圆截得的线段长为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)若![]() 上存在两点
上存在两点![]() ,椭圆
,椭圆![]() 上存在两个点
上存在两个点![]() 满足:
满足: ![]() 三点共线,
三点共线, ![]() 三点共线且
三点共线且![]() ,求四边形
,求四边形![]() 的面积的最小值.
的面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】京剧是我国的国粹,是“国家级非物质文化遗产”,某机构在网络上调查发现各地京剧票友的年龄![]() 服从正态分布
服从正态分布![]() 同时随机抽取
同时随机抽取![]() 位参与某电视台《我爱京剧》节目的票友的年龄作为样本进行分析研究(全部票友的年龄都在
位参与某电视台《我爱京剧》节目的票友的年龄作为样本进行分析研究(全部票友的年龄都在![]() 内),样本数据分别区间为
内),样本数据分别区间为![]() 由此得到如图所示的频率分布直方图.
由此得到如图所示的频率分布直方图.

(Ⅰ) 若![]() 求
求![]() 的值;
的值;
(Ⅱ)现从样本年龄在![]() 的票友中组织了一次有关京剧知识的问答,每人回答一个问题,答对赢得一台老年戏曲演唱机,答错没有奖品,假设每人答对的概率均为
的票友中组织了一次有关京剧知识的问答,每人回答一个问题,答对赢得一台老年戏曲演唱机,答错没有奖品,假设每人答对的概率均为![]() ,且每个人回答正确与否相互之间没有影响,用
,且每个人回答正确与否相互之间没有影响,用![]() 表示票友们赢得老年戏曲演唱机的台数,求
表示票友们赢得老年戏曲演唱机的台数,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】△ABC的内角A,B,C所对的边分别为a,b,c.且 ![]() =(cos(A﹣B),﹣sin(A﹣B)),
=(cos(A﹣B),﹣sin(A﹣B)), ![]() =(cosB,sinB),若
=(cosB,sinB),若 ![]()
![]() =﹣
=﹣ ![]() . (Ⅰ)求sin A的值;
. (Ⅰ)求sin A的值;
(Ⅱ)若a=4 ![]() ,b=5,求向量
,b=5,求向量 ![]() 在
在 ![]() 方向上的投影.
方向上的投影.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着手机的发展,“微信”越来越成为人们交流的一种方式.某机构对“使用微信交流”的态度进行调查,随机抽取了50人,他们年龄的频数分布及对“使用微信交流”赞成人数如下表.
年龄(单位:岁) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) | [65,75) |
频数 | 5 | 10 | 15 | 10 | 5 | 5 |
赞成人数 | 5 | 10 | 12 | 7 | 2 | 1 |
(Ⅰ)若以“年龄45岁为分界点”,由以上统计数据完成下面![]() 列联表,并判断是否有99%的把握认为“使用微信交流”的态度与人的年龄有关;
列联表,并判断是否有99%的把握认为“使用微信交流”的态度与人的年龄有关;
年龄不低于45岁的人数 | 年龄低于45岁的人数 | 合计 | |
赞成 | |||
不赞成 | |||
合计 |
(Ⅱ)若从年龄在[25,35)和[55,65)的被调查人中按照分层抽样的方法选取6人进行追踪调查,并给予其中3人“红包”奖励,求3人中至少有1人年龄在[55,65)的概率.
参考数据如下:
附临界值表:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
![]() 的观测值:
的观测值: ![]() (其中
(其中![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】元旦期间,某轿车销售商为了促销,给出了两种优惠方案,顾客只能选择其中的一种,方案一:每满![]() 万元,可减
万元,可减![]() 千元;方案二:金额超过
千元;方案二:金额超过![]() 万元(含
万元(含![]() 万元),可摇号三次,其规则是依次装有
万元),可摇号三次,其规则是依次装有![]() 个幸运号、
个幸运号、![]() 个吉祥号的一个摇号机,装有
个吉祥号的一个摇号机,装有![]() 个幸运号、
个幸运号、![]() 个吉祥号的二号摇号机,装有
个吉祥号的二号摇号机,装有![]() 个幸运号、
个幸运号、![]() 个吉祥号的三号摇号机各摇号一次,其优惠情况为:若摇出
个吉祥号的三号摇号机各摇号一次,其优惠情况为:若摇出![]() 个幸运号则打
个幸运号则打![]() 折,若摇出
折,若摇出![]() 个幸运号则打
个幸运号则打![]() 折;若摇出
折;若摇出![]() 个幸运号则打
个幸运号则打![]() 折;若没有摇出幸运号则不打折.
折;若没有摇出幸运号则不打折.
(1)若某型号的车正好![]() 万元,两个顾客都选中第二中方案,求至少有一名顾客比选择方案一更优惠的概率;
万元,两个顾客都选中第二中方案,求至少有一名顾客比选择方案一更优惠的概率;
(2)若你评优看中一款价格为![]() 万的便型轿车,请用所学知识帮助你朋友分析一下应选择哪种付款方案.
万的便型轿车,请用所学知识帮助你朋友分析一下应选择哪种付款方案.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com