
分析 根据函数f(x)是增函数,等价为f′(x)≥0在(0,1)上恒成立,即可得到结论.
解答 解:函数的定义域为(0,+∞),要使f(x)=lnx+x2-ax在定义域内是增函数,
则等价为f′(x)≥0在(0,1)上恒成立,
∵f(x)=lnx+x2-ax,
∴f′(x)=$\frac{1}{x}$+2x-a≥0,
即a≤$\frac{1}{x}$+2x在x∈(0,1)上恒成立,
当x>0时,y=$\frac{1}{x}$+2x≥2$\sqrt{2x•\frac{1}{x}}$=2$\sqrt{2}$,当且仅当x=$\frac{\sqrt{2}}{2}$时取等号.
则a≤2$\sqrt{2}$,
故答案为:(-∞,$2\sqrt{2}$].
点评 本题主要考查函数单调性的应用和判断,根据函数导数和单调性之间的关系转化为函数恒成立即可得到结论.


 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p∧q | B. | ¬p∨q | C. | p∧¬q | D. | p∨q |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
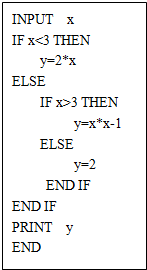
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
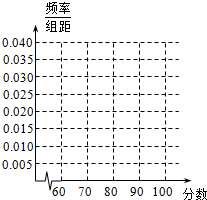 为纪念中国抗日战争胜利70周年,某中学高三年级举办了“铭记历史,开创未来”的抗战历史知识竞赛活动,共有1000名学生参加了这次竞赛.为了解本次竞赛的成绩情况,从中抽取了部分学生的成绩(得分均为整数,满分为100分)进行统计,请你根据频率分布表,解答下列问题:
为纪念中国抗日战争胜利70周年,某中学高三年级举办了“铭记历史,开创未来”的抗战历史知识竞赛活动,共有1000名学生参加了这次竞赛.为了解本次竞赛的成绩情况,从中抽取了部分学生的成绩(得分均为整数,满分为100分)进行统计,请你根据频率分布表,解答下列问题:| 序号 | 分组 | 频数 | 频率 |
| 1 | [60,70) | ① | 0.15 |
| 2 | [70,80) | 20 | 0.2 |
| 3 | [80,90) | 35 | 0.35 |
| 4 | [90,100) | 30 | ② |
| 合计 | 100 | 1 | |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com