练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    给定函数①y=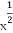,②y=lo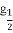(x+1),③y=|x-1|,④y=2x+1,其中在区间(0,1)上是单调递减的函数的序号是(　　)

    (A)①② (B)②③ (C)③④ (D)①④

     

    B

    【解析】①y=在x>0时是增函数,

    ②y=lo(x+1)在x>-1时是减函数.

    ③y=|x-1|在x∈(0,1)时是减函数.

    ④y=2x+1在x∈R上是增函数.

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2014年高考数学文二轮专题复习与测试解答题保分训练练习卷（解析版） 题型：解答题

    已知m＝(2cos x＋2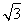sin x,1)，n＝(cos x，－y)，且m⊥n.

    (1)将y表示为x的函数f(x)，并求f(x)的单调递增区间；

    (2)已知a，b，c分别为△ABC的三个内角A，B，C对应的边长，若f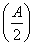＝3，且a＝2，b＋c＝4，求△ABC的面积．

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学全程总复习课时提升作业（八）第二章第五节练习卷（解析版） 题型：解答题

    已知函数f(x)=-x+log2.

    (1)求f()+f(-)的值.

    (2)当x∈(-a,a],其中a∈(0,1),a是常数时,函数f(x)是否存在最小值?若存在,求出f(x)的最小值;若不存在,请说明理由.

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学全程总复习课时提升作业（五）第二章第二节练习卷（解析版） 题型：填空题

    函数f(x)=x2-kx+1在[1,2]上单调,则k的取值范围为　　　　.

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学全程总复习课时提升作业（五）第二章第二节练习卷（解析版） 题型：选择题

    已知函数y=f(x)满足:对任意的x1<x2≤-1,[f(x2)-f(x1)](x2-x1)>0恒成立,则f(-2),f(-),f(-1)的大小关系为(　　)

    (A)f(-2)<f(-)<f(-1)

    (B)f(-2)>f(-)>f(-1)

    (C)f(-2)>f(-1)>f(-)

    (D)f(-)>f(-2)>f(-1)

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学全程总复习课时提升作业（二）第一章第二节练习卷（解析版） 题型：填空题

    有三个命题:(1)“若x+y=0,则x,y互为相反数”的逆命题.

    (2)“若a>b,则a2>b2”的逆否命题.

    (3)“若x≤-3,则x2+x-6>0”的否命题.

    其中真命题的个数为　　　　.

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学全程总复习课时提升作业（二）第一章第二节练习卷（解析版） 题型：选择题

    下列各小题中,p是q的充要条件的是(　　)

    (1)p:m<-2或m>6;q:y=x2+mx+m+3有两个不同的零点.

    (2)p: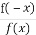=1;q:y=f(x)是偶函数.

    (3)p:cosα=cosβ;q:tanα=tanβ.

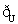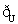    (4)p:A∩B=A;q: B⊆A.

    (A)(1)(2) (B)(2)(3)

    (C)(3)(4) (D)(1)(4)

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学全程总复习课时提升作业（九）第二章第六节练习卷（解析版） 题型：选择题

    实数a=0.,b=log30.3,c=的大小关系正确的是(　　)

    (A)a<c<b (B)a<b<c

    (C)b<a<c (D)b<c<a

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学全程总复习课时提升作业（一）第一章第一节练习卷（解析版） 题型：填空题

    已知集合A={x∈N|∈N},则集合A的所有子集是　　　　　.

     

    查看答案和解析>>

    同步练习册答案