
科目:高中数学 来源: 题型:
| A、3 | B、4 | C、5 | D、6 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x2+ax+2 |
| 1 |
| 3 |
| 11 |
| 3 |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年江西南昌10所省高三第二次模拟冲刺理科数学试卷(二)(解析版) 题型:选择题
下列命题中:①“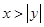 ”是“
”是“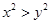 ”的充要条件;
”的充要条件;
②已知随机变量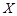 服从正态分布
服从正态分布 ,
,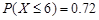 ,则
,则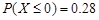 ;
;
③若n组数据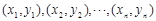 的散点图都在直线
的散点图都在直线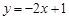 上,则这n组数据的相关系数为
上,则这n组数据的相关系数为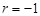 ;
;
④函数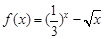 的所有零点存在区间是
的所有零点存在区间是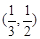 .其中正确的个数是( )
.其中正确的个数是( )
A.1 B.2 C.3 D.4
查看答案和解析>>
科目:高中数学 来源:2011-2012学年江苏省常州中学高三最后冲刺综合练习数学试卷3(文科)(解析版) 题型:解答题
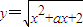 在区间(-∞,1]上是减函数,则实数a∈[-3,-2];
在区间(-∞,1]上是减函数,则实数a∈[-3,-2];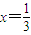 对称.
对称.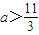 ;
;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com