
在平面直角坐标系中,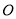 为坐标原点,直线
为坐标原点,直线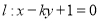 与圆
与圆 相交于
相交于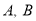 两点,
两点,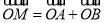 .若点
.若点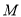 在圆
在圆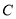 上,则实数
上,则实数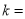 ( )
( )
A.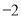 B.
B.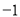 C.
C.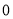 D.
D.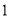
 科学实验活动册系列答案
科学实验活动册系列答案科目:高中数学 来源:2013-2014学年广东省东莞市高三模拟(一)理科数学试卷(解析版) 题型:填空题
已知集合A={x|x2-2x-3>0 },B={x|ax2+bx+c≤0},若A∩B={x|3<x≤4},
A∪B=R,则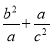 的最小值为____.
的最小值为____.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年山东省青岛市高三4月统一质量检测考试文科数学试卷(解析版) 题型:解答题
已知函数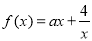 .
.
(1)从区间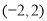 内任取一个实数
内任取一个实数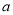 ,设事件
,设事件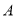 ={函数
={函数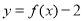 在区间
在区间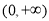 上有两个不同的零点},求事件
上有两个不同的零点},求事件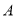 发生的概率;
发生的概率;
(2)若连续掷两次骰子(骰子六个面上标注的点数分别为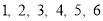 )得到的点数分别为
)得到的点数分别为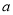 和
和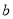 ,记事件
,记事件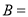 {
{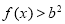 在
在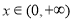 恒成立},求事件
恒成立},求事件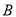 发生的概率.
发生的概率.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年山东省青岛市高三4月统一质量检测考试文科数学试卷(解析版) 题型:选择题
已知定义在实数集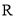 上的偶函数
上的偶函数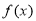 满足
满足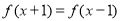 ,且当
,且当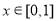 时,
时,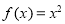 ,则关于
,则关于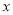 的方程
的方程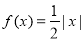 在
在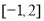 上根的个数是( )
上根的个数是( )
A.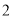 B.
B.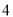 C.
C.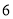 D.
D.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年山东省高三12月月考理科数学试卷(解析版) 题型:解答题
已知函数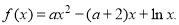
(1)当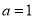 时,求曲线
时,求曲线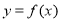 在点
在点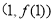 处的切线方程;
处的切线方程;
(2)当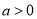 时,若
时,若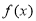 在区间
在区间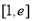 上的最小值为-2,求
上的最小值为-2,求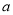 的取值范围;
的取值范围;
(3)若对任意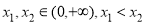 ,且
,且 恒成立,求
恒成立,求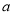 的取值.
的取值.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年山东省高三12月月考文科数学试卷(解析版) 题型:解答题
设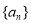 是公比大于
是公比大于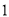 的等比数列,
的等比数列,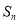 为数列
为数列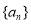 的前
的前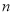 项和.已知
项和.已知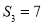 ,且
,且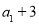 ,
,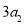 ,
,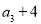 构成等差数列.
构成等差数列.
(1)求数列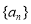 的通项公式;
的通项公式;
(2)令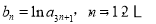 求数列
求数列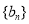 的前
的前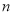 项和
项和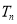 .
.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年山东省菏泽市高三3月模拟考试文科数学试卷(解析版) 题型:解答题
如图;已知椭圆C: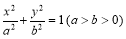 的离心率为
的离心率为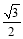 ,以椭圆的左顶点T为圆心作圆T:
,以椭圆的左顶点T为圆心作圆T: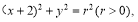 设圆T与椭圆C交于点M、N.
设圆T与椭圆C交于点M、N.
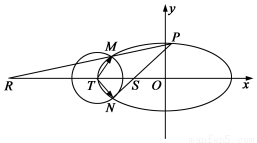
(1)求椭圆C的方程;
(2)求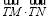 的最小值,并求此时圆T的方程;
的最小值,并求此时圆T的方程;
(3)设点P是椭圆C 上异于M,N的任意一点,且直线MP,NP分别与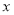 轴交于点R,S,O为坐标原点。求证:
轴交于点R,S,O为坐标原点。求证: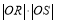 为定值.
为定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com