
【题目】在棱长为1的正方体ABCD-A1B1C1D1中,点A关于平面BDC1对称点为M,则M到平面A1B1C1D1的距离为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】D
【解析】
以D为原点,DA,DC,DD1所在直线分别为x,y,z轴,建立空间直角坐标系,求出平面BDC1的法向量![]() =(1,-1,1),从而平面BDC1的方程为x-y+z=0,进而过点A(1,0,0)且垂直于平面BDC1的直线方程为(x-1)=-y=z,推导出过点A(1,0,0)且垂直于平面BDC1的直线方程与平面BDC1的交点为
=(1,-1,1),从而平面BDC1的方程为x-y+z=0,进而过点A(1,0,0)且垂直于平面BDC1的直线方程为(x-1)=-y=z,推导出过点A(1,0,0)且垂直于平面BDC1的直线方程与平面BDC1的交点为![]() ,得到点A关于平面BDC1对称点M
,得到点A关于平面BDC1对称点M![]() ,由此能求出M到平面A1B1C1D1的距离.
,由此能求出M到平面A1B1C1D1的距离.
以D为原点,DA,DC,DD1所在直线分别为x,y,z轴,建立空间直角坐标系,
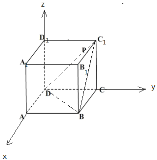
D(0,0,0),B(1,1,0),C1(0,1,1),A(1,0,0),A1(1,0,1),
![]() =(1,1,0),
=(1,1,0),![]() =(0,1,1),
=(0,1,1),
设平面BDC1的法向量![]() =(x,y,z),
=(x,y,z),
则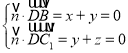 ,取x=1,得
,取x=1,得![]() =(1,-1,1),
=(1,-1,1),
∴平面BDC1的方程为x-y+z=0,
过点A(1,0,0)且垂直于平面BDC1的直线方程为:
(x-1)=-y=z,
令(x-1)=-y=z=t,得x=t+1,y=-t,z=t,
代入平面方程x-y+z=0,得t+1+t+t=0,解得t=![]() ,
,
∴过点A(1,0,0)且垂直于平面BDC1的直线方程与平面BDC1的交点为![]()
∴点A关于平面BDC1对称点M![]() ,
,
![]() ,平面A1B1C1D1的法向量
,平面A1B1C1D1的法向量![]() =(0,0,1),
=(0,0,1),
∴M到平面A1B1C1D1的距离为d=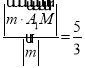
故选:D.


科目:高中数学 来源: 题型:
【题目】设![]() 是不小于3的正整数,集合
是不小于3的正整数,集合![]() ,对于集合
,对于集合![]() 中任意两个元素
中任意两个元素![]() ,
,![]() .
.
定义1:![]() .
.
定义2:若![]() ,则称
,则称![]() ,
,![]() 互为相反元素,记作
互为相反元素,记作![]() ,或
,或![]() .
.
(Ⅰ)若![]() ,
,![]() ,
,![]() ,试写出
,试写出![]() ,
,![]() ,以及
,以及![]() 的值;
的值;
(Ⅱ)若![]() ,证明:
,证明:![]() ;
;
(Ⅲ)设![]() 是小于
是小于![]() 的正奇数,至少含有两个元素的集合
的正奇数,至少含有两个元素的集合![]() ,且对于集合
,且对于集合![]() 中任意两个不相同的元素
中任意两个不相同的元素![]() ,
,![]() ,都有
,都有![]() ,试求集合
,试求集合![]() 中元素个数的所有可能值.
中元素个数的所有可能值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 过点
过点![]() ,其参数方程为
,其参数方程为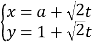 (
(![]() 为参数,
为参数, ![]() ),以
),以![]() 为极点,
为极点, ![]() 轴非负半轴为极轴,建立极坐标系,曲线
轴非负半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)求已知曲线![]() 和曲线
和曲线![]() 交于
交于![]() 两点,且
两点,且![]() ,求实数
,求实数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义变换![]() 将平面内的点
将平面内的点![]() 变换到平面内的点
变换到平面内的点![]() ;若曲线
;若曲线![]() 经变换
经变换![]() 后得到曲线
后得到曲线![]() ,曲线
,曲线![]() 经变换
经变换![]() 后得到曲线
后得到曲线![]() ,…,依次类推,曲线
,…,依次类推,曲线![]() 经变换
经变换![]() 后得到曲线
后得到曲线![]() ,当
,当![]() 时,记曲线
时,记曲线![]() 与
与![]() 、
、![]() 轴正半轴的交点为
轴正半轴的交点为![]() 和
和![]() ,某同学研究后认为曲线
,某同学研究后认为曲线![]() 具有如下性质:①对任意的
具有如下性质:①对任意的![]() ,曲线
,曲线![]() 都关于原点对称;②对任意的
都关于原点对称;②对任意的![]() ,曲线
,曲线![]() 恒过点
恒过点![]() ;③对任意的
;③对任意的![]() ,曲线
,曲线![]() 均在矩形
均在矩形![]() (含边界)的内部,其中
(含边界)的内部,其中![]() 的坐标为
的坐标为![]() ;④记矩形
;④记矩形![]() 的面积为
的面积为![]() ,则
,则![]() ;其中所有正确结论的序号是_______.
;其中所有正确结论的序号是_______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ex+1-alnax+a(a>0).
(1)当a=1时,求曲线y=f(x)在点(1,f(1))处的切线方程;
(2)若关于x的不等式f(x)>0恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,以原点O为极点,x轴的正半轴为极轴建立极坐标系,两种坐标系中取相同的长度单位.已知直线l的参数方程为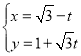 (t为参数),曲线C的极坐标方程为ρ=4sin(θ+
(t为参数),曲线C的极坐标方程为ρ=4sin(θ+![]() ).
).
(1)求直线l的普通方程与曲线C的直角坐标方程;
(2)若直线l与曲线C交于M,N两点,求△MON的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着科技的发展,网购已经逐渐融入了人们的生活.在家里面不用出门就可以买到自己想要的东西,在网上付款即可,两三天就会送到自己的家门口,如果近的话当天买当天就能送到,或者第二天就能送到,所以网购是非常方便的购物方式.某公司组织统计了近五年来该公司网购的人数![]() (单位:人)与时间
(单位:人)与时间![]() (单位:年)的数据,列表如下:
(单位:年)的数据,列表如下:
| 1 | 2 | 3 | 4 | 5 |
| 24 | 27 | 41 | 64 | 79 |
(1)依据表中给出的数据,是否可用线性回归模型拟合![]() 与
与![]() 的关系,请计算相关系数
的关系,请计算相关系数![]() 并加以说明(计算结果精确到0.01).(若
并加以说明(计算结果精确到0.01).(若![]() ,则线性相关程度很高,可用线性回归模型拟合)
,则线性相关程度很高,可用线性回归模型拟合)
附:相关系数公式
 ,参考数据
,参考数据![]() .
.
(2)建立![]() 关于
关于![]() 的回归方程,并预测第六年该公司的网购人数(计算结果精确到整数).
的回归方程,并预测第六年该公司的网购人数(计算结果精确到整数).
(参考公式:
 ,
,![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com