
【题目】若数列![]() 满足:存在正整数T,对于任意正整数n都有
满足:存在正整数T,对于任意正整数n都有![]() 成立,则称数列
成立,则称数列![]() 为周期数列,周期为T.已知数列
为周期数列,周期为T.已知数列![]() 满足
满足![]() ,
, ,则下列结论中错误的是( )
,则下列结论中错误的是( )
A.若![]() ,则m可以取3个不同的值;
,则m可以取3个不同的值;
B.若![]() ,则数列
,则数列![]() 是周期为3的数列;
是周期为3的数列;
C.对于任意的![]() 且T≥2,存在
且T≥2,存在![]() ,使得
,使得![]() 是周期为
是周期为![]() 的数列
的数列
D.存在![]() 且
且![]() ,使得数列
,使得数列![]() 是周期数列
是周期数列
【答案】D
【解析】
A. 若![]() ,根据
,根据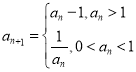 ,分别对
,分别对![]() 讨论求解即可; B.若
讨论求解即可; B.若![]() ,根据
,根据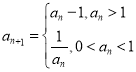 ,分别求得
,分别求得![]() 即可判断; C.通过B判断即可;D.用反证法判断.
即可判断; C.通过B判断即可;D.用反证法判断.
A.若![]() ,因为
,因为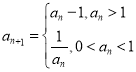 ,
,
当![]() 时,
时,![]() ,解得
,解得![]() ,当
,当![]() 时,
时,![]() ,解得
,解得![]() ,当
,当![]() 时,
时,![]() ,解得
,解得![]() ,
,
当![]() 时,
时,![]() ,解得
,解得![]() ,当
,当![]() 时,
时,![]() ,解得
,解得![]() ,当
,当![]() 时,
时,![]() ,解得
,解得![]() ,不合题意,故m可以取3个不同的值,故正确;
,不合题意,故m可以取3个不同的值,故正确;
B.若![]() ,则
,则![]() ,所以
,所以![]() ,则数列
,则数列![]() 是周期为3的数列,故正确;
是周期为3的数列,故正确;
C.对于任意的![]() 且T≥2,存在
且T≥2,存在![]() ,使得
,使得![]() 是周期为
是周期为![]() 的数列,其否定为:.对于任意的
的数列,其否定为:.对于任意的![]() 且T≥2,不存在
且T≥2,不存在![]() ,使得
,使得![]() 是周期为
是周期为![]() 的数列,由B知原命题正确;
的数列,由B知原命题正确;
D.假设存在![]() 且
且![]() ,使得数列
,使得数列![]() 是周期数列,当
是周期数列,当![]() 时,
时,![]() ,此时,数列
,此时,数列![]() 不是周期数列,
不是周期数列,
当![]() 时,当
时,当![]() 时,
时,![]() ,
,![]() ,若
,若![]() ,
,![]() ,则
,则![]() ,即
,即![]() ,而
,而![]() 不为平方数,因此假设不正确,故数列
不为平方数,因此假设不正确,故数列![]() 不是周期数列,故错误.
不是周期数列,故错误.
故选:D


科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,离心率为
,离心率为![]() ,过右焦点
,过右焦点![]() 作直线
作直线![]() 交椭圆
交椭圆![]() 于
于![]() ,
,![]() 两点,
两点,![]() 的周长为
的周长为![]() ,点
,点![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设直线![]() 、
、![]() 的斜率
的斜率![]() ,
,![]() ,请问
,请问![]() 是否为定值?若是定值,求出其定值;若不是,说明理由.
是否为定值?若是定值,求出其定值;若不是,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】节约资源和保护环境是中国的基本国策.某化工企业,积极响应国家要求,探索改良工艺,使排放的废气中含有的污染物数量逐渐减少.已知改良工艺前所排放的废气中含有的污染物数量为![]() ,首次改良后所排放的废气中含有的污染物数量为
,首次改良后所排放的废气中含有的污染物数量为![]() .设改良工艺前所排放的废气中含有的污染物数量为
.设改良工艺前所排放的废气中含有的污染物数量为![]() ,首次改良工艺后所排放的废气中含有的污染物数量为
,首次改良工艺后所排放的废气中含有的污染物数量为![]() ,则第
,则第![]() 次改良后所排放的废气中的污染物数量
次改良后所排放的废气中的污染物数量![]() ,可由函数模型
,可由函数模型![]() 给出,其中
给出,其中![]() 是指改良工艺的次数.
是指改良工艺的次数.
(1)试求改良后所排放的废气中含有的污染物数量的函数模型;
(2)依据国家环保要求,企业所排放的废气中含有的污染物数量不能超过![]() ,试问至少进行多少次改良工艺后才能使得该企业所排放的废气中含有的污染物数量达标.(参考数据:取
,试问至少进行多少次改良工艺后才能使得该企业所排放的废气中含有的污染物数量达标.(参考数据:取![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
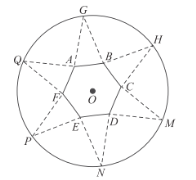
【题目】如图,圆形纸片的圆心为O,半径为5cm,该纸片上的正六边形ABCDEF的中心为O,G、H、M、N、P、Q为圆O上的点,△GAB,△HBC,△MCD,△NDE,△PEF,△QAF分别是以AB,BC,CD,DE,EF,FA为底边的等腰三角形,沿虚线剪开后,分别以AB,BC,CD,DE,EF,FA为折痕折起△GAB,△HBC,△MCD,△NDE,△PEF,△QAF,使得G、H、M、N、P、Q重合,得到六棱锥.当正六边形ABCDEF的边长变化时,所得六棱锥体积(单位:cm3)的最大值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(文)(2017·衡水二模)某商场在元旦举行购物抽奖促销活动,规定顾客从装有编号0,1,2,3,4的五个相同小球的抽奖箱中一次任意摸出两个小球,若取出的两个小球的编号之和等于7则中一等奖,等于6或5则中二等奖,等于4则中三等奖,其余结果为不中奖.
(1)求中二等奖的概率.
(2)求不中奖的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com