
【题目】已知函数f(x)=lnx+ax2+ax.
(1)若曲线y=f(x)在点P(1,f(1))处的切线与直线y=4x+1平行,求实数a的值;
(2)若![]() 时,关于x的方程
时,关于x的方程![]() 在(0,2]上恰有两个不相等的实数根,求实数b的取值范围.
在(0,2]上恰有两个不相等的实数根,求实数b的取值范围.
【答案】(1)a=1.(2)[ln2﹣5,![]() ).
).
【解析】
(1)求导后![]() ,进行求解
,进行求解![]() ;(2)分离参数通过画出新函数图象,根据直线和函数图象有两个交点求出实数b的取值范围.
;(2)分离参数通过画出新函数图象,根据直线和函数图象有两个交点求出实数b的取值范围.
(1)由题意,f′(x)![]() 2ax+a,x>0.
2ax+a,x>0.
根据题意,有f′(1)=3a+1=4,
解得a=1.
(2)由题意,f(x)=lnx![]() x2
x2![]() x,
x,
则lnx![]() x2
x2![]() x
x![]() x+b,
x+b,
即b=lnx![]() x2
x2![]() x,
x,
令g(x)=lnx![]() x2
x2![]() x,x>0.则
x,x>0.则
g′(x)![]() x
x![]() .
.
令g′(x)=0,解得x=1,或x=2;
令g′(x)>0,解得0<x<1,或x>2;
令g′(x)<0,解得1<x<2.
∴函数g(x)在(0,1)上单调递增,在(1,2)上单调递减,
在x=1处取得极大值g(1)![]() ,
,
在x=2处取得极小值g(2)=ln2﹣5.
故函数g(x)在(0,2]上大致图象如下:
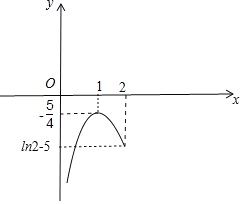
根据题意及图,可知
实数b的取值范围为:[ln2﹣5,![]() ).
).


 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案科目:高中数学 来源: 题型:
【题目】实数a,b满足ab>0且a≠b,由a、b、![]() 、
、![]() 按一定顺序构成的数列( )
按一定顺序构成的数列( )
A. 可能是等差数列,也可能是等比数列
B. 可能是等差数列,但不可能是等比数列
C. 不可能是等差数列,但可能是等比数列
D. 不可能是等差数列,也不可能是等比数列
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】 已知抛物线![]() 的顶点为坐标原点
的顶点为坐标原点![]() ,焦点
,焦点![]() 在
在![]() 轴的正半轴上,过点
轴的正半轴上,过点![]() 的直线
的直线![]() 与抛物线相交于
与抛物线相交于![]() ,
,![]() 两点,且满足
两点,且满足![]()
(1)求抛物线![]() 的方程;
的方程;
(2)若![]() 是抛物线
是抛物线![]() 上的动点,点
上的动点,点![]() 在
在![]() 轴上,圆
轴上,圆![]() 内切于
内切于![]() ,求
,求![]() 面积的最小值.
面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于定义域为R的函数![]() ,若函数
,若函数![]() 是奇函数,则称
是奇函数,则称![]() 为正弦奇函数.已知
为正弦奇函数.已知![]() 是单调递增的正弦奇函数,其值域为R,
是单调递增的正弦奇函数,其值域为R,![]() .
.
(1)已知![]() 是正弦奇函数,证明:“
是正弦奇函数,证明:“![]() 为方程
为方程![]() 的解”的充要条件是“
的解”的充要条件是“![]() 为方程
为方程![]() 的解”;
的解”;
(2)若![]()
![]() ,求
,求![]() 的值;
的值;
(3)证明:![]() 是奇函数.
是奇函数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设m,n是两条不同直线,α,β,γ是三个不同平面,给出下列四个命题:
①若m⊥α,n⊥α,则m∥n;②若α∥β,β∥γ,m⊥α,则m⊥γ;
③若m∥α,n∥α,则m∥n;④若m⊥α,m∥β,则α⊥β.
其中正确命题的个数是( )
A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了鼓励职员工作热情,某公司对每位职员一年来的工作业绩按月进行考评打分;年终按照职员的月平均值评选公司最佳职员并给予相应奖励.已知职员![]() 一年来的工作业绩分数的茎叶图如图所示:
一年来的工作业绩分数的茎叶图如图所示:
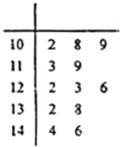
(1)根据职员![]() 的业绩茎叶图求出他这一年的工作业绩的中位数和平均数;
的业绩茎叶图求出他这一年的工作业绩的中位数和平均数;
(2)由于职员![]() 的业绩高,被公司评为年度最佳职员,在公司年会上通过抽奖形式领取奖金.公司准备了六张卡片,其中一张卡片上标注奖金为6千元,两张卡片的奖金为4千元,另外三张的奖金为2千元.规则是:获奖职员
的业绩高,被公司评为年度最佳职员,在公司年会上通过抽奖形式领取奖金.公司准备了六张卡片,其中一张卡片上标注奖金为6千元,两张卡片的奖金为4千元,另外三张的奖金为2千元.规则是:获奖职员![]() 需要从六张卡片中随机抽出两张,这两张卡片上的金额数之和作为奖金数.求职员
需要从六张卡片中随机抽出两张,这两张卡片上的金额数之和作为奖金数.求职员![]() 获得奖金6千元的概率;并说明获得奖金6千元和8千元哪个可能性较大?
获得奖金6千元的概率;并说明获得奖金6千元和8千元哪个可能性较大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在圆![]() 上任取一点
上任取一点![]() ,过点
,过点![]() 作
作![]() 轴的垂线段
轴的垂线段![]() ,
,![]() 为垂足,当点
为垂足,当点![]() 在圆上运动时,点
在圆上运动时,点![]() 在线段
在线段![]() 上,且
上,且![]() ,点
,点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)过抛物线![]() :
:![]() 的焦点
的焦点![]() 作直线
作直线![]() 交抛物线于
交抛物线于![]() ,
,![]() 两点,过
两点,过![]() 且与直线
且与直线![]() 垂直的直线交曲线
垂直的直线交曲线![]() 于另一点
于另一点![]() ,求
,求![]() 面积的最小值,以及取得最小值时直线
面积的最小值,以及取得最小值时直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,当
,当![]() ,
,![]() 时,
时,![]() 的值域为
的值域为![]() ,
,![]() ,当
,当![]() ,
,![]() 时,
时,![]() 的值域为
的值域为![]() ,
,![]() ,依此类推,一般地,当
,依此类推,一般地,当![]() ,
,![]() 时,
时,![]() 的值域为
的值域为![]() ,
,![]() ,其中
,其中![]() 、
、![]() 为常数,且
为常数,且![]() ,
,![]() .
.
(1)若![]() ,求数列
,求数列![]() ,
,![]() 的通项公式;
的通项公式;
(2)若![]() ,问是否存在常数
,问是否存在常数![]() ,使得数列
,使得数列![]() 满足
满足![]() ?若存在,求
?若存在,求![]() 的值;若不存在,请说明理由;
的值;若不存在,请说明理由;
(3)若![]() ,设数列
,设数列![]() ,
,![]() 的前
的前![]() 项和分别为
项和分别为![]() ,
,![]() ,求
,求![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com