
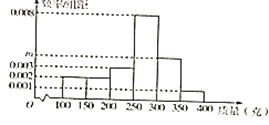
【题目】炎炎夏季,水蜜桃成为备受大家欢迎的一种水果,某果园的水蜜桃质量分布如图所示.
(Ⅰ)求m的值;
(Ⅱ)以频率估计概率,若从该果园中随机采摘5个水蜜桃,记质量在300克以上(含300克)的个数为X,求X的分布列及数学期望;
(Ⅲ)经市场调查,该种水蜜桃在过去50天的销售量(单位:千克)和价格(单位:元/千克)均为销售时间t(天)的函数,且销售量近似地满足f(t)=﹣3t+300(1≤t≤50,t∈N),前30天价格为g(t)=![]() +20(1≤t≤30,t∈N),后20天价格为g(t)=30(31≤t≤50,t∈N),求日销售额S的最大值.
+20(1≤t≤30,t∈N),后20天价格为g(t)=30(31≤t≤50,t∈N),求日销售额S的最大值.
【答案】(Ⅰ)0.004;(Ⅱ)分布列见解析,数学期望![]() ;(Ⅲ)6400.
;(Ⅲ)6400.
【解析】
(Ⅰ)利用频率和为1列方程求出m的值;
(Ⅱ)由题意知随机变量X服从二项分布,由计算对应的概率值,写出分布列和数学期望值;
(Ⅲ)根据题意列出S的解析式,计算t为何值时S取得最大值.
(Ⅰ)根据频率分布直方图知,
(0.002+0.002+0.003+0.008+m+0.001)×50=1,
解得m=0.004;
(Ⅱ)随机采摘1个水蜜桃,其质量在300克以上(含300克)的概率为![]() ,
,
且X的可能取值为0,1,2,3,4,5,
则P(X=0)=![]() =
=![]() ,
,
P(X=1)=![]()
![]()
![]() =
=![]() ,
,
P(X=2)=![]()
![]()
![]() =
=![]() ,
,
P(X=3)=![]()
![]()
![]() =
=![]() ,
,
P(X=4)=![]()
![]()
![]() =
=![]() ,
,
P(X=5)=![]() =
=![]() ;
;
∴X的分布列为
X | 0 | 1 | 2 | 3 | 4 | 5 |
P |
|
|
|
|
|
|
数学期望为E(X)=5×![]() =
=![]() ;
;
(Ⅲ)根据题意知,S= ;
;
当1≤t≤30,t∈N时,S=(﹣3t+300)(![]() t+20)=﹣t2+40t+6000,
t+20)=﹣t2+40t+6000,
∴t=20时,S取得最大值为6400;
当31≤t≤50,t∈N时,S=30(﹣3t+300)=﹣90t+9000为减函数,
∴当t=31时,S取得最大值为6210;
由6400>6210,
∴当t=20时,日销售额S取得最大值为6400.


科目:高中数学 来源: 题型:
【题目】已知函数![]()
(1)求证:![]()
(2)若函数![]() 的图象与直线
的图象与直线![]() 没有交点,求实数
没有交点,求实数![]() 的取值范围;
的取值范围;
(3)若函数![]() ,则是否存在实数
,则是否存在实数![]() ,使得
,使得![]() 的最小值为
的最小值为![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一台机器使用的时间较长,但还可以使用,它按不同的转速生产出来的某机械零件有一些会有缺点,每小时生产有缺点零件的多少,随机器的运转的速度而变化,下表为抽样试验的结果:
转速x(转/秒) | 2 | 4 | 5 | 6 | 8 |
每小时生产有缺点的零件数y(件) | 30 | 40 | 60 | 50 | 70 |
(1)画散点图;
(2)如果y对x有线性相关关系,求回归直线方程;
(3)若实际生产中,允许每小时的产品中有缺点的零件最多为89个,那么机器的运转速度应控制在什么范围内?(参考数值:![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】曲线C1的参数方程为![]() (θ为参数),将曲线C1上所有点的横坐标伸长为原来的2倍,纵坐标伸长为原来的
(θ为参数),将曲线C1上所有点的横坐标伸长为原来的2倍,纵坐标伸长为原来的![]() 倍,得到曲线C2.以平面直角坐标系xOy的原点O为极点,x轴的正半轴为极轴,取相同的单位长度建立极坐标系,已知直线l:ρ(cosθ-2sinθ)=6.
倍,得到曲线C2.以平面直角坐标系xOy的原点O为极点,x轴的正半轴为极轴,取相同的单位长度建立极坐标系,已知直线l:ρ(cosθ-2sinθ)=6.
(1)求曲线C2和直线l的普通方程.
(2)P为曲线C2上任意一点,求点P到直线l的距离的最值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2+2﹣alnx﹣bx(a>0).
(Ⅰ)若a=1,b=3,求函数y=f(x)在(1,f(1))处的切线方程;
(Ⅱ)若f(x1)=f(x2)=0,且x1≠x2,证明:f′(![]() )>0.
)>0.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C的中心在坐标原点,焦点在x轴上,椭圆C的离心率为![]() ,且椭圆C过点
,且椭圆C过点![]() .
.
(1)求椭圆C的标准方程:
(2)若直线l:![]() 与椭圆C相交于A,B两点(A,B不是左右顶点),且以
与椭圆C相交于A,B两点(A,B不是左右顶点),且以![]() 为直径的圆过椭圆C的右顶点,求证:直线l过定点,并求出该定点的坐标.
为直径的圆过椭圆C的右顶点,求证:直线l过定点,并求出该定点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两人2013-2017这五年的年度体检的血压值的折线图如图所示.

(1)根据散点图,直接判断甲、乙这五年年度体检的血压值谁的波动更大,并求波动更大者的方差;
(2)根据乙这五年年度体检血压值的数据,求年度体检血压值![]() 关于年份
关于年份![]() 的线性回归方程,并据此估计乙在2018年年度体检的血压值.
的线性回归方程,并据此估计乙在2018年年度体检的血压值.
(附: ,
,![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com