垂直于同一个平面的两条直线平行． （填写对号或错号）．
【答案】
分析：设直线a、b都与平面α垂直，并假设a、b不平行，再作出辅助线和辅助平面，结合线面垂直的定义和平行线的性质，可以证出经过空间一点有两条直线与已知直线垂直，得到与公理矛盾，所以原假设不成立，从而得到原命题是真命题．
解答：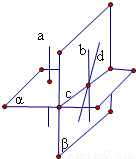
解：设直线a、b都与平面α垂直，可以用反证法证明a、b必定是平行直线
假设a、b不平行，过直线b与平面α的交点作直线d，使d∥a
∴直线d与直线b是相交直线，设它们确定平面β，且β∩α=c
∵b⊥α，c?α，∴b⊥c．同理可得a⊥c，
又∵d∥a，∴d⊥c
这样经过一点作出两条直线b、d都与直线c垂直，这是不可能的
∴假设不成立，故原命题是真命题
故答案为：√
点评：本题要求我们证明空间直线与平面垂直的性质定理，着重考查了反证法的思路和线面垂直的定义等知识点，属于基础题．
