
【题目】数列{![]() }满足
}满足![]()
(1)若{![]() }是等差数列,求其通项公式;
}是等差数列,求其通项公式;
(2)若{![]() }满足
}满足![]() 为{
为{![]() }的前
}的前![]() 项和,求
项和,求![]() .
.
【答案】(1)![]() (2)
(2)![]() =
=![]()
【解析】
(1)由等差数列的定义,若数列{an}是等差数列,则an=a1+(n﹣1)d,an+1=a1+nd.结合an+1+an=4n﹣3,得即可解得首项a1的值;(2)由an+1+an=4n﹣3(n∈N*),用n+1代n得an+2+an+1=4n+1(n∈N*).两式相减,得an+2﹣an=4.从而得出数列{a2n﹣1}是首项为a1,公差为4的等差数列.进一步得到数列{a2n}是首项为a2,公差为4的等差数列.对n进行分类讨论求得通项公式,再分组求和即可;
(1)若数列{an}是等差数列,则an=a1+(n﹣1)d,an+1=a1+nd.
由an+1+an=4n﹣3,得(a1+nd)+[a1+(n﹣1)d]=4n﹣3,即2d=4,2a1﹣d=﹣3,解得d=2,a1![]() .故
.故![]()
(2)∵![]() ,∴
,∴![]()
又∵![]() ,∴数列的奇数项与偶数项分别成等差数列,公差均为4
,∴数列的奇数项与偶数项分别成等差数列,公差均为4
∴![]() ,
,![]()
![]()
=![]()
=![]()


 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:高中数学 来源: 题型:
【题目】今年年初,我国多个地区发生了持续性大规模的雾霾天气,给我们的身体健康产生了巨大的威胁.私家车的尾气排放也是造成雾霾天气的重要因素之一,因此在生活中我们应该提倡低碳生活,少开私家车,尽量选择绿色出行方式,为预防雾霾出一份力.为此,很多城市实施了机动车车尾号限行,我市某报社为了解市区公众对“车辆限行”的态度,随机抽查了50人,将调查情况进行整理后制成下表:
年龄(岁) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) | [65,75] |
频数 | 5 | 10 | 15 | 10 | 5 | 5 |
赞成人数 | 4 | 6 | 9 | 6 | 3 | 4 |
(Ⅰ)完成被调查人员的频率分布直方图;
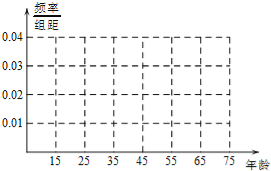
(Ⅱ)若从年龄在[15,25),[25,35)的被调查者中各随机选取两人进行进行追踪调查,记选中的4人中不赞成“车辆限行”的人数为ξ,求随机变量ξ的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下图是某省从1月21日至2月24日的新冠肺炎每日新增确诊病例变化曲线图.

若该省从1月21日至2月24日的新冠肺炎每日新增确诊人数按日期顺序排列构成数列![]() ,
,![]() 的前n项和为
的前n项和为![]() ,则下列说法中正确的是( )
,则下列说法中正确的是( )
A.数列![]() 是递增数列B.数列
是递增数列B.数列![]() 是递增数列
是递增数列
C.数列![]() 的最大项是
的最大项是![]() D.数列
D.数列![]() 的最大项是
的最大项是![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】节约资源和保护环境是中国的基本国策.某化工企业,积极响应国家要求,探索改良工艺,使排放的废气中含有的污染物数量逐渐减少.已知改良工艺前所排放的废气中含有的污染物数量为![]() ,首次改良后所排放的废气中含有的污染物数量为
,首次改良后所排放的废气中含有的污染物数量为![]() .设改良工艺前所排放的废气中含有的污染物数量为
.设改良工艺前所排放的废气中含有的污染物数量为![]() ,首次改良工艺后所排放的废气中含有的污染物数量为
,首次改良工艺后所排放的废气中含有的污染物数量为![]() ,则第
,则第![]() 次改良后所排放的废气中的污染物数量
次改良后所排放的废气中的污染物数量![]() ,可由函数模型
,可由函数模型![]() 给出,其中
给出,其中![]() 是指改良工艺的次数.
是指改良工艺的次数.
(1)试求改良后所排放的废气中含有的污染物数量的函数模型;
(2)依据国家环保要求,企业所排放的废气中含有的污染物数量不能超过![]() ,试问至少进行多少次改良工艺后才能使得该企业所排放的废气中含有的污染物数量达标.(参考数据:取
,试问至少进行多少次改良工艺后才能使得该企业所排放的废气中含有的污染物数量达标.(参考数据:取![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com