Question

设椭圆

x2

a2

+

y2

b2

=1（a＞b＞0）的左、右焦点分别为F₁，F₂，A是椭圆上的一点，AF₂⊥F₁F₂，原点O到直线AF₁的距离为

1

3

|OF1|．
（I）证明：a=

2

b；
（II）设Q₁，Q₂为椭圆上的两个动点，OQ₁⊥OQ₂，过原点O作直线Q₁Q₂的垂线OD，垂足为D，求点D的轨迹方程．

Answer 1

分析：（1）先求得A点的坐标，再求得直线AF1的方程，利用点到直线的距离结合条件得到一个关于a，b的关系式，化简即得；
（2）设点D的坐标为（x₀，y₀）．欲求其轨迹方程，即寻找x，y的关系式，由直线Q₁Q₂的方程和椭圆的方程组成方程组，结合向量的垂直关系即可找到找x，y的关系式，从而问题解决．

解答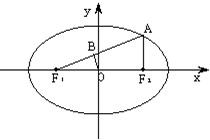：解：（I）由题设AF₂⊥F₁F₂及F₁（-c，0），F₂（c，0），
不妨设点A（c，y），其中y＞0．
由于点A在椭圆上，有

c2

a2

+

y2

b2

=1，即

a2-b2

a2

+

y2

b2

=1．
解得y=

b2

a

，从而得到A(c，

b2

a

)．
直线AF₁的方程为y=

b2

2ac

(x+c)，整理得b²x-2acy+b²c=0．
由题设，原点O到直线AF₁的距离为

1

3

|OF1|，即

c

3

=

b2c

b4+4a2c2

，
将c²=a²-b²代入上式并化简得a²=2b²，即a=

2

b．

（II）设点D的坐标为（x₀，y₀）．当y₀≠0时，由OD⊥Q₁Q₂知，直线Q₁Q₂的斜率为-

x0

y0

，
所以直线Q₁Q₂的方程为y=-

x0

y0

(x-x0)+y0，或y=kx+m，其中k=-

x0

y0

，m=y0+

x 2 0

y0

．
点Q₁（x₁，y₁），Q₂（x₂，y₂）的坐标满足方程组

y=kx+m ① x2+2y2=2b2 ②

将①式代入②式，得x²+2（kx+m）²=2b²．
整理得（1+2k²）x²+4kmx+2m²-2b²=0．
于是x1+x2=-

4km

1+2k2

，x1．x2=

2m2-2b2

1+2k2

．③
由①式得y₁y₂=（kx₁+m）（kx₂+m）=k²x₁x₂+km（x₁+x₂）+m²=k2.

2m2-2b2

1+2k2

+km.

-4km

1+2k2

+m2=

m3-2b2k2

1+2k2

．④
由OQ₁⊥OQ₂知x₁x₂+y₁y₂=0．将③式和④式代入得

3m2-2b2-2b2k2

1+2k2

=0，3m²=2b²（1+k²）．
将k=-

x0

y0

，m=y0+

x 2 0

y0

代入上式，整理得

x

2 0

+

y

2 0

=

2

3

b2．
当y₀=0时，直线Q₁Q₂的方程为x=x₀．点Q₁（x₁，y₀），Q₂（x₂，y₂）的坐标满足方程组

x=x0 x2+2y2=2b2

所以x1=x2=x0，y1，2=±

2b2- x 2 0 2

．
由OQ₁⊥OQ₂知x₁x₂+y₁y₂=0，即

x

2 0

-

2b2- x 2 0

2

=0，解得

x

2 0

=

2

3

b2
这时，点D的坐标仍满足

x

2 0

+

y

2 0

=

2

3

b2．
综上，点D的轨迹方程为x2+y2=

2

3

b2．

点评：本小题主要考查椭圆的标准方程和几何性质、直线方程、求曲线的方程等基础知识，考查曲线和方程的关系等解析几何的基本思想方法及推理、运算能力．