
(1)设第n次是由甲投掷的概率为Pn,求Pn;
(2)前三次投掷中,恰好甲投掷两次的概率是多少?
答案:(1)两颗骰子向上的点数之和为3的倍数的情况有1+2,1+5,2+1,2+4,3+3,3+6,4+2,4+5,5+1,5+4,6+3,6+6共12种.所以投掷一次向上点数之和为3的倍数的概率是![]() .
.
又“第n次由甲投掷”这一事件包括“第n-1次由甲投掷,第n次仍由甲投掷”和“第n-1次由乙投掷,第n次由甲投掷”两种情形,
∴Pn=![]() Pn-1+(1
Pn-1+(1![]() )(1-Pn-1)=
)(1-Pn-1)=![]() Pn-1
Pn-1![]() Pn
Pn![]() (Pn-1
(Pn-1![]() ).
).
于是{Pn![]() }是公比为
}是公比为![]() 的等比数列,从而Pn
的等比数列,从而Pn![]() =(P1
=(P1![]() )·(
)·(![]() )n-1.
)n-1.
∵P1=1,∴Pn![]() .
.
故Pn=![]() [1+(
[1+(![]() )n-1].
)n-1].
(2)由(1)知,P1=1,P2=![]() ,P3=
,P3=![]() ,
,
由于规定第一次是甲投掷,所以前三次投掷中甲恰好投掷两次的情形只有两种:
甲甲乙,甲乙甲,因而其概率为
P=1×![]() .
.


科目:高中数学 来源:2010年广东省中山市高一下学期期末模拟考试数学卷 题型:解答题
(9分)甲、乙两位同学报名参加2010年在广州举办的亚运会志愿者服务,两人条件相当,但名额只有一人. 两人商量采用抛骰子比大小的方法决定谁去,每人将一颗质地均匀的正方体骰子(六个面的点数分别为1,2,3,4,5,6)先后抛掷两次, 两次点数和较大的当选志愿者. 甲先抛掷两次,第1次向上点数为3,第2次向上点数为4.
(1)记乙第一次出现的点数为 ,第二次出现的点数为
,第二次出现的点数为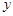 ,用
,用 表示先后抛掷两次的结果,试写出两次向上点数和与甲相同的所有可能结果.
表示先后抛掷两次的结果,试写出两次向上点数和与甲相同的所有可能结果.
(2)求乙抛掷两次后,向上点数和与甲相同的概率?
(3)求乙抛掷两次后,能决定乙当选志愿者的概率?
查看答案和解析>>
科目:高中数学 来源:广东省中山市08-09学年高一下学期期末考试 题型:解答题
甲、乙两位同学报名参加2010年在广州举办的亚运会志愿者服务,两人条件相当,但名额只有一人. 两人商量采用抛骰子比大小的方法决定谁去,每人将一颗质地均匀的正方体骰子(六个面的点数分别为1,2,3,4,5,6)先后抛掷两次, 两次点数和较大的当选志愿者. 甲先抛掷两次,第1次向上点数为3,第2次向上点数为4.
(1)记乙第一次出现的点数为 ,第二次出现的点数为
,第二次出现的点数为 ,用
,用 表示先后抛掷两次的结果,试写出两次向上点数和与甲相同的所有可能结果.
表示先后抛掷两次的结果,试写出两次向上点数和与甲相同的所有可能结果.
(2)求乙抛掷两次后,向上点数和与甲相同的概率?
(3)求乙抛掷两次后,能决定乙当选志愿者的概率?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com