
求证:如果两个平面互相垂直,那么经过第一个平面内的一点而垂直于第二个平面的直线在第一个平面内.已知;α⊥β,α∩β=CD,AÎ
a,AB⊥β.求证:AB a.
a.
|
证明:如图,在平面 a内作AE⊥CD.则AE⊥β,而AB⊥β.∴AB与AE重合.∵AE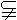 a,∴AB a,∴AB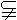 a. a.
(1) 本题的结论可以直接应用;(2)本题的证法采用的是同一法.同一法的一般过程:①不从已知条件入手,而另作图形使它具有求证的结论中所提的特性;②证明所作用的图形特性,与已知条件符合;③因为已知条件和求证的结论所指的事物都是唯一的,从而推出所作的图形与已知条件来求的是同一个东西,由此断定原命题成立.反证法与同一法都是间接证法,但前者证的是原命题的逆合题;后者证的是原命题的逆命题,但原命题必须符合同一法则.由于同一法则不易掌握,所以遇到有可能利用同一法证明的题,可改为用反证法形式证明.如上例可假设AB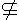 a,在平面a内作AE⊥CD,得AE⊥β,又AB⊥β与这一点只有一条直线与平面垂直矛盾,所以假设不成立,得AB a,在平面a内作AE⊥CD,得AE⊥β,又AB⊥β与这一点只有一条直线与平面垂直矛盾,所以假设不成立,得AB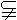 a. a. |


 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案科目:高中数学 来源: 题型:047
求证:如果两个平面互相垂直,那么经过第一个平面内的一点而垂直于第二个平面的直线在第一个平面内.已知;
α⊥β,α∩β=CD,AÎ a,AB⊥β.求证:AB a.
a.查看答案和解析>>
科目:高中数学 来源: 题型:
给出下列四个命题:
①经过平面外一点有且仅有一个平面与已知平面垂直;②如果一条直线和两个垂直平面中的一个垂直,它必和另一个平行;③过不在平面内的一条直线可作无数个平面与已知平面垂直;④如果两个平面互相垂直,经过一个平面内一点与另一个平面垂直的直线在这个平面内.其中正确的是________.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年贵州省遵义四中高一下学期期末考试数学 题型:单选题
“如果一条直线与一个平面垂直,则称这条直线与这个平面构成一组正交线面对;如果两个平面互相垂直,则称这两个平面构成一组正交平面对.”在正方体的12条棱和6个表面中,能构成正交线面对和正交平面对的组数分别是( )
A. 和 和 | B. 和 和 | C. 和 和 | D. 和 和 |
查看答案和解析>>
科目:高中数学 来源:2013届贵州省高一下学期期末考试数学 题型:选择题
“如果一条直线与一个平面垂直,则称这条直线与这个平面构成一组正交线面对;如果两个平面互相垂直,则称这两个平面构成一组正交平面对.”在正方体的12条棱和6个表面中,能构成正交线面对和正交平面对的组数分别是( )
(A) 和
和 (B)
(B) 和
和 (C)
(C) 和
和 (D)
(D) 和
和
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com