
【题目】设函数f(x)=x2+2ax﹣a﹣1,x∈[0,2],a为常数.
(1)用g(x)表示f(x)的最小值,求g(a)的解析式;
(2)在(1)中,是否存在最小的整数m,使得g(a)﹣m≤0对于任意a∈R均成立,若存在,求出m的值;若不存在,请说明理由.
【答案】
(1)解:对称轴 x=﹣a,
①当﹣a<0即a>0 时,函数f(x)=x2+2ax﹣a﹣1,x∈[0,2]上是增函数,
当x=0 时有最小值 f(0)=﹣a﹣1
②当﹣a≥2即a≤﹣2 时,函数f(x)=x2+2ax﹣a﹣1,x∈[0,2]上是减函数,
x=2时有最小值,f(2)=3a+3
③当0<﹣a<2即﹣2<a<0 时,函数f(x)=x2+2ax﹣a﹣1,x∈[0,2]上是不单调,
x=﹣a时有最小值 f(﹣a)=﹣a2﹣a﹣1
∴g(a)= 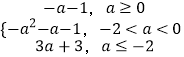
(2)解:存在,由题知g(a)在(﹣∞, ![]() )是增函数,在[
)是增函数,在[ ![]() ,+∞)是减函数
,+∞)是减函数
a= ![]() 时,g(a)max=﹣
时,g(a)max=﹣ ![]()
g(a)﹣m≤0恒成立,可得g(a)max≤m,∴ ![]()
∵m为整数,∴m的最小值为0
【解析】(1)先根据二次函数的对称轴对a进行分类讨论,结合函数的单调性进而求得g(a)的解析式;(2)根据(1)中g(a)的解析式判断其单调区间,再求得g(a)的最大值,由g(a)﹣m≤0恒成立,可得g(a)max≤m即可求得整数m的最小值.
【考点精析】认真审题,首先需要了解二次函数的性质(增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小).


 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案科目:高中数学 来源: 题型:
【题目】已知过点A(﹣4,0)的动直线l与抛物线C:x2=2py(p>0)相交于B、C两点.
(1)当l的斜率是![]() 时,
时, ![]() ,求抛物线C的方程;
,求抛物线C的方程;
(2)设BC的中垂线在y轴上的截距为b,求b的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn , a1=1,an≠0,anan+1=4Sn﹣1.
(Ⅰ)求{an}的通项公式;
(Ⅱ)证明: ![]() +
+ ![]() +…+
+…+ ![]() <2.
<2.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(理科)已知函数f(x)=4x3+3tx2﹣6t2x+t﹣1,x∈R,t∈R.
(1)当t≠0时,求f(x)的单调区间;
(2)证明:对任意t∈(0,+∞),f(x)在区间(0,1)内均存在零点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=xlnx﹣ax2+(2a﹣1)x,a∈R.
(1)令g(x)为f(x)的导函数,求g(x)单调区间;
(2)已知函数f(x)在x=1处取得极大值,求实数a取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题:
①α>β的充分不必要条件是sinα>sinβ
②若a,b∈R,ab<0,则 ![]()
③命题“若x+y≠5,则x≠2或y≠3”的否命题为假命题
④若a≠b,则a3+b3>a2b+ab2
其中真命题的序号是 . (请把所有真命题的序号都填上)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知圆M:(x+1)2+y2= ![]() 的圆心为M,圆N:(x﹣1)2+y2=
的圆心为M,圆N:(x﹣1)2+y2= ![]() 的圆心为N,一动圆与圆M内切,与圆N外切.
的圆心为N,一动圆与圆M内切,与圆N外切.
(Ⅰ)求动圆圆心P的轨迹方程;
(Ⅱ)过点(1,0)的直线l与曲线P交于A,B两点,若 ![]() =﹣2,求直线l的方程.
=﹣2,求直线l的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com