
【题目】在平面直角坐标系xOy中,点A在y轴正半轴上,点Pn在x轴上,其横坐标为xn , 且{xn} 是首项为1、公比为2的等比数列,记∠PnAPn+1=θn , n∈N* . 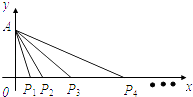
(1)若 ![]() ,求点A的坐标;
,求点A的坐标;
(2)若点A的坐标为(0,8 ![]() ),求θn的最大值及相应n的值.
),求θn的最大值及相应n的值.
【答案】
(1)解:设A(0,t)(t>0),根据题意,xn=2n﹣1.
由 ![]() ,知
,知 ![]() ,
,
而tanθ3=tan(∠OAP4﹣∠OAP3)= 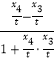 =
= ![]() ,
,
所以 ![]() ,解得t=4或t=8.
,解得t=4或t=8.
故点A的坐标为(0,4)或(0,8).
(2)解:由题意,点Pn的坐标为(2n﹣1,0),tan∠OAPn= ![]() .
.
∴tanθn=tan(∠OAPn+1﹣∠OAPn)= 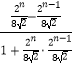 =
= 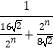 .
.
因为 ![]() ≥
≥ ![]() ,所以tanθn≤
,所以tanθn≤ ![]() =
= ![]() ,
,
当且仅当 ![]() ,即n=4时等号成立.
,即n=4时等号成立.
∵0<θn< ![]() ,y=tanx在(0,
,y=tanx在(0, ![]() )上为增函数,
)上为增函数,
∴当n=4时,θn最大,其最大值为 ![]() .
.
【解析】(1)利用{xn} 是首项为1、公比为2的等比数列,确定通项,利用差角的正切公式,建立方程,即可求得A的坐标;(2)表示出tanθn=tan(∠OAPn+1﹣∠OAPn),利用基本不等式,结合正切函数的单调性,即可求得结论.
【考点精析】关于本题考查的基本不等式和两角和与差的正切公式,需要了解基本不等式:![]()
![]() ,(当且仅当
,(当且仅当![]() 时取到等号);变形公式:
时取到等号);变形公式:![]()
![]() ;两角和与差的正切公式:
;两角和与差的正切公式:![]() 才能得出正确答案.
才能得出正确答案.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知二次函数f(x)=x2+bx+c有两个零点1和﹣1.
(1)求f(x)的解析式;
(2)设g(x)![]() ,试判断函数g(x)在区间(﹣1,1)上的单调性并用定义证明;
,试判断函数g(x)在区间(﹣1,1)上的单调性并用定义证明;
(3)由(2)函数g(x)在区间(﹣1,1)上,若实数t满足g(t﹣1)﹣g(﹣t)>0,求t的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2sin(ωx),其中常数ω>0
(1)若y=f(x)在[﹣ ![]() ,
, ![]() ]上单调递增,求ω的取值范围;
]上单调递增,求ω的取值范围;
(2)令ω=2,将函数y=f(x)的图象向左平移 ![]() 个单位,再向上平移1个单位,得到函数y=g(x)的图象,区间[a,b](a,b∈R,且a<b)满足:y=g(x)在[a,b]上至少含有30个零点.在所有满足上述条件的[a,b]中,求b﹣a的最小值.
个单位,再向上平移1个单位,得到函数y=g(x)的图象,区间[a,b](a,b∈R,且a<b)满足:y=g(x)在[a,b]上至少含有30个零点.在所有满足上述条件的[a,b]中,求b﹣a的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着手机的普及,大学生迷恋手机的现象非常严重.为了调查双休日大学生使用手机的时间,某机构采用不记名方式随机调查了使用手机时间不超过![]() 小时的
小时的![]() 名大学生,将
名大学生,将![]() 人使用手机的时间分成
人使用手机的时间分成![]() 组:
组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分别加以统计,得到下表,根据数据完成下列问题:
分别加以统计,得到下表,根据数据完成下列问题:
使用时间/时 |
|
|
|
|
|
大学生/人 |
|
|
|
|
|
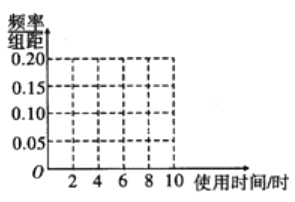
(1)完成频率分布直方图;
(2)根据频率分布直方图估计大学生使用手机的平均时间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设z1 , z2是复数,则下列命题中的假命题是( )
A.若|z1﹣z2|=0,则 ![]() =
= ![]()
B.若z1= ![]() ,则
,则 ![]() =z2
=z2
C.若|z1|=|z2|,则z1? ![]() =z2?
=z2? ![]()
D.若|z1|=|z2|,则z12=z22
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=alnx-bx2(x>0),若函数f(x)在x=1处与直线y=-![]() 相切。
相切。
(1)求实数a,b的值;
(2)求函数f(x)在![]() 上的最大值。
上的最大值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,设
,设![]() 的外接圆圆心为
的外接圆圆心为![]() .
.
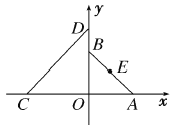
(1)若![]() 与直线
与直线![]() 相切,求实数
相切,求实数![]() 的值;
的值;
(2)设点![]() 在
在![]() 上,使
上,使![]() 的面积等于12的点
的面积等于12的点![]() 有且只有三个,试问这样的
有且只有三个,试问这样的![]() 是否存在?若存在求出
是否存在?若存在求出![]() 的标准方程;若不存在,说明理由.
的标准方程;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com