分析:(Ⅰ)连AC,BD,A1C1,则O为AC,BD的交点,易知四边形A1OCO1为平行四边形,则A1O||O1C,而A1O⊥平面ABCD则O1C⊥平面ABCD,又O1C?平面O1DC,满足面面垂直的判定定理可得结论;
(Ⅱ)作EH⊥平面ABCD,垂足为H,则EH||A1O,点H在直线AC上,且EF在平面ABCD上的射影为HF.由三垂线定理及其逆定理,知EF⊥AD则CF=2BF,从而可知当F为BC的三等分点(靠近B)时,有EF⊥AD;
(III)过点O作OM⊥AA1,垂足为M,连接BM,由三垂线定理得AA1⊥MB∴∠OMB为二面角C-AA1-B的平面角,在三角形OMB中求出此角即可.
解答:
解:(Ⅰ)连AC,BD,A
1C
1,则O为AC,BD的交点,
O
1为A
1C
1,B
1D
1的交点.
由平行六面体的性质知:A
1O
1||OC且A
1O
1=OC
∴四边形A
1OCO
1为平行四边形,A
1O||O
1C
又∵A
1O⊥平面ABCD∴O
1C⊥平面ABCD
又∵O
1C?平面O
1DC∴平面O
1DC⊥平面ABCD
(Ⅱ)作EH⊥平面ABCD,垂足为H,则EH||A
1O,点H在直线AC上,
且EF在平面ABCD上的射影为HF.
由三垂线定理及其逆定理,知EF⊥AD?FH||AB∵AE=2EA
1,∴AH=2HO,从而CH=2AH.又∵HF||AB,∴CF=2BF
从而EF⊥AD?CF=2BF∴当F为BC的三等分点(靠近B)时,有EF⊥AD
(III)过点O作OM⊥AA
1,垂足为M,连接BM.∵A
1O⊥平面ABCD,∴A
1O⊥OB
又∵OB⊥OA∴OB⊥平面A
1AO.由三垂线定理得AA
1⊥MB∴∠OMB为二面角C-AA
1-B的平面角.
在Rt△AMB中,∠MAB=60°,∴
MB=AB又∵
BO=AB,∴
sin∠OMB=∴
∠OMB=arcsin二面角C-AA
1-B的大小为
arcsin 点评:本题主要考查了面面垂直的判定和二面角的度量,求解二面角的关键是寻找二面角的平面角,同时考查了推理能力和计算能力,属于中档题.

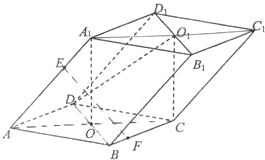 已知平行六面体ABCD-A1B1C1D1的底面为正方形,O1,O分别为上、下底面的中心,且A1在底面ABCD的射影是O.
已知平行六面体ABCD-A1B1C1D1的底面为正方形,O1,O分别为上、下底面的中心,且A1在底面ABCD的射影是O. 解:(Ⅰ)连AC,BD,A1C1,则O为AC,BD的交点,
解:(Ⅰ)连AC,BD,A1C1,则O为AC,BD的交点,

 名题金卷系列答案
名题金卷系列答案 优加精卷系列答案
优加精卷系列答案 如图,已知平行六面体ABC-A1B1C1的底面为正方形,O1,O分别为上、下底面中心,且A1在底面ABCD上的射影为O.
如图,已知平行六面体ABC-A1B1C1的底面为正方形,O1,O分别为上、下底面中心,且A1在底面ABCD上的射影为O. 如图,已知平行六面体ABCD-A1B1C1D1.
如图,已知平行六面体ABCD-A1B1C1D1.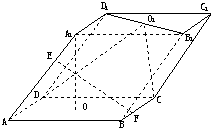 如图,已知平行六面体ABC-A1B1C1的底面为正方形,O1,O分别为上、下底面中心,且A1在底面ABCD上的射影为O.
如图,已知平行六面体ABC-A1B1C1的底面为正方形,O1,O分别为上、下底面中心,且A1在底面ABCD上的射影为O. 如图,已知平行六面体ABCD-A1B1C1D1.
如图,已知平行六面体ABCD-A1B1C1D1.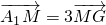 ,设
,设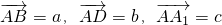 ,用向量a、b、c表示向量
,用向量a、b、c表示向量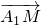 ;
;