练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】如图所示，已知⊙O的半径是1，点C在直径AB的延长线上，BC=1，点P是⊙O上半圆上的一个动点，以PC为边作等边三角形PCD，且点D与圆心分别在PC的两侧．

    (1)若∠POB=θ，试将四边形OPDC的面积y表示为关于θ的函数；

    (2)求四边形OPDC面积的最大值．

    【答案】(1) (2) 2+

    【解析】试题分析：（1）第（1）问，先利用余弦定理求出再利用分割的方法求四边形OPDC的面积表达式. (2)第（2）问，利用三角函数的图像和性质求函数y的最大值.

    试题解析:

    (1)在△POC中，由余弦定理得PC2=OP2+OC2—2OP·OC·cosθ=5—4cosθ.

    所以y=S△OPC+S△PCD .

    (2)当，即时ymax=2+.

    答：四边形OPDC面积的最大值为2+.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知圆C：x2+y2+2x-4y+3=0．
    （1）若圆C的切线在x轴、y轴上的截距相等，求切线的方程；
    （2）从圆C外一点P（x1 ， y1）向圆引一条切线，切点为M，O为坐标原点，且有|PM|=|PO|，求使|PM|最小的点P的坐标．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】数独游戏越来越受人们喜爱，今年某地区科技馆组织数独比赛，该区甲、乙、丙、丁四所学校的学生积极参赛，参赛学生的人数如表所示：

    中学

    甲

    乙

    丙

    丁

    人数

    30

    40

    20

    10

    为了解参赛学生的数独水平，该科技馆采用分层抽样的方法从这四所中学的参赛学生中抽取30名参加问卷调查．
    （Ⅰ）问甲、乙、丙、丁四所中学各抽取多少名学生？
    （Ⅱ）从参加问卷调查的30名学生中随机抽取2名，求这2名学生来自同一所中学的概率；
    （Ⅲ）在参加问卷调查的30名学生中，从来自甲、丙两所中学的学生中随机抽取2名，用X表示抽得甲中学的学生人数，求X的分布列．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】若离散型随机变量ξ的概率分布如表所示，则a的值为（ ）

    ξ

    ﹣1

    1

    P

    4a﹣1

    3a2+a


    A.
    B.﹣2
    C. 或﹣2
    D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在三棱锥S﹣ABC中，SB⊥底面ABC，且SB=AB=2，BC= ，D、E分别是SA、SC的中点．

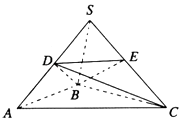
    （I）求证：平面ACD⊥平面BCD；
    （II）求二面角S﹣BD﹣E的平面角的大小．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f(x)＝

    (1)试比较f(f(－3))与f(f(3))的大小；

    (2)画出函数的图象；

    (3)若f(x)＝1，求x的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知数列{an}，{bn}满足2Sn=（an+2）bn ， 其中Sn是数列{an}的前n项和．
    （1）若数列{an}是首项为 ，公比为﹣ 的等比数列，求数列{bn}的通项公式；
    （2）若bn=n，a2=3，求证：数列{an}满足an+an+2=2an+1 ， 并写出数列{an}的通项公式；
    （3）在（2）的条件下，设cn= ， 求证：数列{cn}中的任意一项总可以表示成该数列其他两项之积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知四边形ABCD内接于圆O

    (1)若AB=2,BC=6,CD=4,AC=8,求BD

    (2)若AC=,BC=+1,∠ADB=,求AD2+DC2的取值范围

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】锐角△ABC中，角A、B、C所对的边分别为a、b、c，且tanA﹣tanB= （1+tanAtanB）．
    （Ⅰ）若c2=a2+b2﹣ab，求角A、B、C的大小；
    （Ⅱ）已知向量 =（sinA，cosA）， =（cosB，sinB），求|3 ﹣2 |的取值范围．

    查看答案和解析>>

    同步练习册答案