
【题目】某客户准备在家中安装一套净水系统,该系统为二级过滤,使用寿命为十年如图所示两个二级过滤器采用并联安装,再与一级过滤器串联安装.
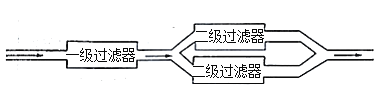
其中每一级过滤都由核心部件滤芯来实现在使用过程中,一级滤芯和二级滤芯都需要不定期更换(每个滤芯是否需要更换相互独立).若客户在安装净水系统的同时购买滤芯,则一级滤芯每个160元,二级滤芯每个80元.若客户在使用过程中单独购买滤芯则一级滤芯每个400元,二级滤芯每个200元.现需决策安装净水系统的同时购买滤芯的数量,为此参考了根据100套该款净水系统在十年使用期内更换滤芯的相关数据制成的图表,其中表1是根据100个一级过滤器更换的滤芯个数制成的频数分布表,图2是根据200个二级过滤器更换的滤芯个数制成的条形图.
表1:一级滤芯更换频数分布表
一级滤芯更换的个数 | 8 | 9 |
频数 | 60 | 40 |
图2:二级滤芯更换频数条形图
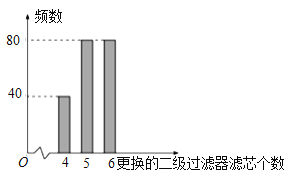
以100个一级过滤器更换滤芯的频率代替1个一级过滤器更换滤芯发生的概率,以200个二级过滤器更换滤芯的频率代替1个二级过滤器更换滤芯发生的概率.
(1)求一套净水系统在使用期内需要更换的各级滤芯总个数恰好为16的概率;
(2)记![]() 表示该客户的净水系统在使用期内需要更换的二级滤芯总数,求
表示该客户的净水系统在使用期内需要更换的二级滤芯总数,求![]() 的分布列及数学期望;
的分布列及数学期望;
(3)记![]() 分别表示该客户在安装净水系统的同时购买的一级滤芯和二级滤芯的个数.若
分别表示该客户在安装净水系统的同时购买的一级滤芯和二级滤芯的个数.若![]() ,且
,且![]() ,以该客户的净水系统在使用期内购买各级滤芯所需总费用的期望值为决策依据,试确定
,以该客户的净水系统在使用期内购买各级滤芯所需总费用的期望值为决策依据,试确定![]() 的值.
的值.
【答案】(1)0.024;(2)分布列见解析,![]() ;(3)
;(3)![]()
【解析】
(1)由题意可知,若一套净水系统在使用期内需要更换的各级滤芯总个数恰好为16,则该套净水系统中一个一级过滤器需要更换8个滤芯,两个二级过滤器均需要更换4个滤芯,而由一级滤芯更换频数分布表和二级滤芯更换频数条形图可知,一级过滤器需要更换8个滤芯的概率为0.6,二级过滤器需要更换4个滤芯的概率为0.2,再由乘法原理可求出概率;
(2)由二级滤芯更换频数条形图可知,一个二级过滤器需要更换滤芯的个数为4,5,6的概率分别为0.2,0.4,0.4,而![]() 的可能取值为8,9,10,11,12,然后求出概率,可得到
的可能取值为8,9,10,11,12,然后求出概率,可得到![]() 的分布列及数学期望;
的分布列及数学期望;
(3)由![]() ,且
,且![]() ,可知若
,可知若![]() ,则
,则![]() ,或若
,或若![]() ,则
,则![]() ,再分别计算两种情况下的所需总费用的期望值比较大小即可.
,再分别计算两种情况下的所需总费用的期望值比较大小即可.
(1)由题意知,若一套净水系统在使用期内需要更换的各级滤芯总个数恰好为16,则该套净水系统中一个一级过滤器需要更换8个滤芯,两个二级过滤器均需要更换4个滤芯,设“一套净水系统在使用期内需要更换的各级滤芯总个数恰好为16”为事件![]() ,
,
因为一个一级过滤器需要更换8个滤芯的概率为0.6,二级过滤器需要更换4个滤芯的概率为0.2,所以![]() .
.
(2)由柱状图知,一个二级过滤器需要更换滤芯的个数为4,5,6的概率分别为0.2,0.4,0.4,由题意![]() 的可能取值为8,9,10,11,12,
的可能取值为8,9,10,11,12,
从而![]() ,
,
![]() ,
,
![]() .
.
所以![]() 的分布列为
的分布列为
| 8 | 9 | 10 | 11 | 12 |
| 0.04 | 0.16 | 0.32 | 0.32 | 0.16 |
![]() (个).
(个).
或用分数表示也可以为
| 8 | 9 | 10 | 11 | 12 |
|
|
|
|
|
|
![]() (个).
(个).
(3)解法一:记![]() 表示该客户的净水系统在使用期内购买各级滤芯所需总费用(单位:元)
表示该客户的净水系统在使用期内购买各级滤芯所需总费用(单位:元)
因为![]() ,且
,且![]() ,
,
1°若![]() ,则
,则![]() ,
,
![]() (元);
(元);
2°若![]() ,则
,则![]() ,
,
![]() (元).
(元).
因为![]() ,故选择方案:
,故选择方案:![]() .
.
解法二:记![]() 分别表示该客户的净水系统在使用期内购买一级滤芯和二级滤芯所需费用(单位:元)
分别表示该客户的净水系统在使用期内购买一级滤芯和二级滤芯所需费用(单位:元)
1°若![]() ,则
,则![]() ,
,
![]() 的分布列为
的分布列为
| 1280 | 1680 |
| 0.6 | 0.4 |
| 880 | 1080 |
| 0.84 | 0.16 |
该客户的净水系统在使用期内购买的各级滤芯所需总费用为![]() (元);
(元);
2°若![]() ,则
,则![]() ,
,
![]() 的分布列为
的分布列为
| 800 | 1000 | 1200 |
| 0.52 | 0.32 | 0.16 |
![]() (元).
(元).
因为![]()
所以选择方案:![]() .
.


 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:高中数学 来源: 题型:
【题目】传染病的流行必须具备的三个基本环节是:传染源、传播途径和人群易感性.三个环节必须同时存在,方能构成传染病流行.呼吸道飞沫和密切接触传播是新冠状病毒的主要传播途径,为了有效防控新冠状病毒的流行,人们出行都应该佩戴口罩.某地区已经出现了新冠状病毒的感染病人,为了掌握该地区居民的防控意识和防控情况,用分层抽样的方法从全体居民中抽出一个容量为100的样本,统计样本中每个人出行是否会佩戴口罩的情况,得到下面列联表:
戴口罩 | 不戴口罩 | |
青年人 | 50 | 10 |
中老年人 | 20 | 20 |
(1)能否有![]() 的把握认为是否会佩戴口罩出行的行为与年龄有关?
的把握认为是否会佩戴口罩出行的行为与年龄有关?
(2)用样本估计总体,若从该地区出行不戴口罩的居民中随机抽取5人,求恰好有2人是青年人的概率.
附: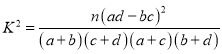
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】百年大计,教育为本.某校积极响应教育部号召,不断加大拔尖人才的培养力度,为清华、北大等排名前十的名校输送更多的人才.该校成立特长班进行专项培训.据统计有如下表格.(其中![]() 表示通过自主招生获得降分资格的学生人数,
表示通过自主招生获得降分资格的学生人数,![]() 表示被清华、北大等名校录取的学生人数)
表示被清华、北大等名校录取的学生人数)
年份(届) | 2014 | 2015 | 2016 | 2017 | 2018 |
| 41 | 49 | 55 | 57 | 63 |
| 82 | 96 | 108 | 106 | 123 |
(1)通过画散点图发现![]() 与
与![]() 之间具有线性相关关系,求
之间具有线性相关关系,求![]() 关于
关于![]() 的线性回归方程;(保留两位有效数字)
的线性回归方程;(保留两位有效数字)
(2)若已知该校2019年通过自主招生获得降分资格的学生人数为61人,预测2019年高考该校考人名校的人数;
(3)若从2014年和2018年考人名校的学生中采用分层抽样的方式抽取出5个人回校宣传,在选取的5个人中再选取2人进行演讲,求进行演讲的两人是2018年毕业的人数![]() 的分布列和期望.
的分布列和期望.
参考公式: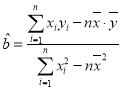 ,
,![]()
参考数据:![]() ,
,![]() ,
,![]() ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
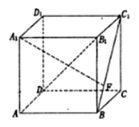
【题目】如图,在正方体![]() 中,点
中,点![]() 是线段
是线段![]() 上的动点,则下列说法正确的是( )
上的动点,则下列说法正确的是( )
A.无论点![]() 在
在![]() 上怎么移动,都有
上怎么移动,都有![]()
B.当点![]() 移动至
移动至![]() 中点时,才有
中点时,才有![]() 与
与![]() 相交于一点,记为点
相交于一点,记为点![]() ,且
,且![]()
C.无论点![]() 在
在![]() 上怎么移动,异面直线
上怎么移动,异面直线![]() 与
与![]() 所成角都不可能是
所成角都不可能是![]()
D.当点![]() 移动至
移动至![]() 中点时,直线
中点时,直线![]() 与平面
与平面![]() 所成角最大且为
所成角最大且为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,直线
轴的正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 交曲线
交曲线![]() 于
于![]() 两点,
两点,![]() 为
为![]() 中点.
中点.
(1)求曲线![]() 的直角坐标方程和点
的直角坐标方程和点![]() 的轨迹
的轨迹![]() 的极坐标方程;
的极坐标方程;
(2)若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某鲜花店根据以往某品种鲜花的销售记录,绘制出日销售量的频率分布直方图,如图所示.将日销售量落入各组区间的频率视为概率,且假设每天的销售量相互独立.

(1)求在未来的连续4天中,有2天的日销售量低于100枝且另外2天不低于150枝的概率;
(2)用![]() 表示在未来4天里日销售量不低于100枝的天数,求随机变量
表示在未来4天里日销售量不低于100枝的天数,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com