
分析 (1)根据题意得圆心到切线的距离即为圆的半径,利用点到直线的距离公式求出,写出圆的标准方程即可;
(2)求出圆心坐标,即可求出圆的标准方程.
解答 解:(1)∵圆心到切线的距离d=r,即r=d=$\frac{|3+35+2|}{\sqrt{{1}^{2}+{7}^{2}}}$=4$\sqrt{2}$,圆心C(3,-5),
∴圆C方程为(x-3)2+(y+5)2=32;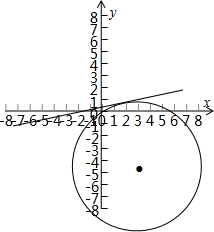
(2)∵圆心在y轴上,∴设圆心为(0,b)
又∵半径是5,且与直线y=6相切,
∴圆心(0,b)到直线y=6的距离等于半径5,即|b-6|=5
解得b=11或1,
∴圆心为(0,1)或(0,11)
∴圆的方程为x2+(y-1)2=25 或x2+(y-11)2=25
点评 此题考查了圆的标准方程,求出圆的圆心、半径是解本题的关键.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
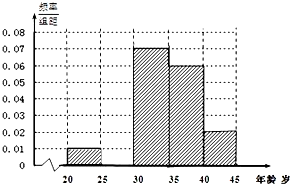 2015年7月16日,电影《捉妖记》上映,上映至今全国累计票房已超过20亿,某影院为了解观看此部电影的观众年龄的情况,在某场次的100名观众中随机调查了20名观众,已知抽到的观众年龄可分成5组:[20,25),[25,30),[30,35),[35,40),[40,45),根据调查结果得出年龄情况残缺的频率分布直方图如图所示.
2015年7月16日,电影《捉妖记》上映,上映至今全国累计票房已超过20亿,某影院为了解观看此部电影的观众年龄的情况,在某场次的100名观众中随机调查了20名观众,已知抽到的观众年龄可分成5组:[20,25),[25,30),[30,35),[35,40),[40,45),根据调查结果得出年龄情况残缺的频率分布直方图如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3x-4y=0或x=0 | B. | 4x-3y=0 | ||
| C. | 3x-4y=0或4x-3y=0 | D. | 3x-4y=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{{m}^{n}}$ | B. | $\frac{1}{{n}^{m}}$ | C. | $\frac{1}{{m}^{n-1}}$ | D. | $\frac{1}{{n}^{m-1}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5$\sqrt{2}$-1 | B. | $\sqrt{17}$+2 | C. | 6-2$\sqrt{2}$ | D. | $\sqrt{10}$+3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com